题目内容
5.若y=2asin(2x-$\frac{π}{3}$)+b,x∈[0,$\frac{π}{2}$]的最大值是1,最小值是-5,求a,b的值.分析 先求出当x∈[0,$\frac{π}{2}$]时,sin(2x-$\frac{π}{3}$)的取值范围讨论a,建立方程关系进行求解即可.
解答 解:∵x∈[0,$\frac{π}{2}$],
∴2x∈[0,π],
2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
则sin(2x-$\frac{π}{3}$)∈[sin(-$\frac{π}{3}$),sin$\frac{π}{2}$],
即sin(2x-$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],
∵当x∈[0,$\frac{π}{2}$]的最大值是1,最小值是-5,
∴若a≥0,则$\left\{\begin{array}{l}{2a+b=1}\\{-\frac{\sqrt{3}}{2}×2a+b=-5}\end{array}\right.$,得$\left\{\begin{array}{l}{2a+b=1}\\{-\sqrt{3}a+b=-5}\end{array}\right.$,得a=6(2-$\sqrt{3}$)=12-6$\sqrt{3}$,b=-23+12$\sqrt{3}$,
若a<0,则$\left\{\begin{array}{l}{2a+b=-5}\\{-\sqrt{3}a+b=1}\end{array}\right.$,得a=-6(2-$\sqrt{3}$)=6$\sqrt{3}$-12,b=25-12$\sqrt{3}$.
点评 本题主要考查三角函数最值的应用,根据条件建立方程关系是解决本题的关键.注意要对a进行分类讨论.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.定义{x,y}max=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若a=tanθ,b=sinθ,c=cosθ,θ∈{θ|-$\frac{π}{4}$<θ<$\frac{3}{4}$π,θ≠0,$\frac{π}{4}$,$\frac{π}{2}$}且{a,b}max=a,{b,c}max=b,则θ的取值范围是( )
| A. | (-$\frac{π}{4}$,0) | B. | (0,$\frac{π}{4}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{π}{2}$,$\frac{3}{4}$π) |
17.已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为$\frac{1}{4}$.
14.空间四点中,无三点共线是四点共面的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要 |
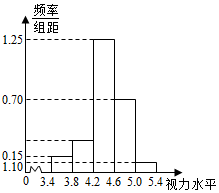 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.