题目内容
18.已知二次函数f(x)=x2+mx+n.(1)若f(x)是偶函数且最小值为1,求f(x)的解析式;
(2)在(1)的前提下,函数$g(x)=\frac{6x}{f(x)}$,解关于x的不等式g(2x)>2x;
(3)函数h(x)=|f(x)|,若x∈[-1,1]时h(x)的最大值为M,且M≥k对任意实数m,n恒成立,求k的最大值.
分析 (1)利用偶函数的定义和函数的最值即可求出函数的解析式,
(2)设t=2x,t>0,原不等式化为t<$\sqrt{5}$,即可求出不等式的解集,
(3)分别赋值x=0,-1,1时,即可求出k的最大值.
解答 解:(1)∵f(x)是偶函数,
∴f(-x)=f(x),
∴x2-mx+n=x2+mx+n,
∴m=0,
∵f(x)是偶函数且最小值为1,
∴n=1
∴f(x)=x2+1,
(2)∵$g(x)=\frac{6x}{f(x)}$=$\frac{6x}{{x}^{2}+1}$,g(2x)>2x,设t=2x,t>0,
∴$\frac{6t}{{t}^{2}+1}$>t,
∴t2<5,
∴t<$\sqrt{5}$,
∴2x<$\sqrt{5}$,
解得x<$\frac{1}{2}$log25,
故解集是$\left\{{\left.x\right|x<\frac{1}{2}{{log}_2}5}\right\}$
(3)令x=1,则|1+m+n|≤M,则-M≤1+m+n≤M①
令x=-1,则|1-m+n|≤M,则-M≤1-m+n≤M②
令x=0,则|n|≤M,则-M≤n≤M③
由①+②-2×③得,$M≥\frac{1}{2}$.当且仅当$m=0,n=-\frac{1}{2}$时等号成立.
因此${k_{max}}=\frac{1}{2}$.
点评 本题考查的知识点是函数奇偶性的性质,函数解析式的求法,以及不等式的解集,以及函数恒成立的问题,属于中档题.

练习册系列答案
相关题目
6.化简$\sqrt{1-{{sin}^2}{{140}°}}$=( )
| A. | ±cos40° | B. | cos40° | C. | -cos40° | D. | ±|cos40°| |
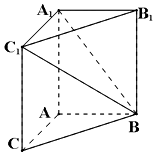 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.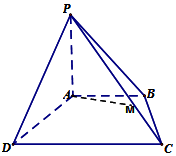 四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.
四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.