题目内容
6.设函数f(x)=cos(2x+$\frac{2π}{3}$)+2cos2x,x∈R.(1)求函数f(x)的最小正周期和单调增区间;
(2)将函数f(x)的图象向右平移$\frac{π}{3}$个单位长度后得到函数g(x)的图象,求函数g(x)在区间$[{0,\frac{π}{2}}]$上的值域.
分析 (1)利用三角函数的恒等变换化简函数的解析式,再利用余弦函数的周期性和单调性,得出结论.
(2)利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用余弦函数的定义域和值域,求得g(x)在区间[0,$\frac{π}{2}$]上的值域.
解答 解:(1)函数f(x)=cos(2x+$\frac{2π}{3}$)+2cos2x=cos2xcos$\frac{2π}{3}$-sin2xsin$\frac{2π}{3}$+cos2x+1
=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+1=cos(2x+$\frac{π}{3}$)+1,
故函数的最小正周期为T=$\frac{2π}{2}$=π,
令2kπ+π≤2x+$\frac{π}{3}$≤2kπ+2π,求得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,求得函数的增区间为[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z.
(2)将函数f(x)的图象向右平移$\frac{π}{3}$个单位长度后得到函数g(x)=cos[2(x-$\frac{π}{3}$)+$\frac{π}{3}$]+1
=cos(2x-$\frac{2π}{3}$+$\frac{π}{3}$)+1=cos(2x-$\frac{π}{3}$)+1的图象,
由x∈[0,$\frac{π}{2}$],可得:2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
可得:cos(2x-$\frac{π}{3}$)∈[-$\frac{1}{2}$,1],
解得:g(x)=cos(2x-$\frac{π}{3}$)+1∈[$\frac{1}{2}$,2].
点评 本题主要考查三角函数的恒等变换,余弦函数的周期性和单调性,函数y=Asin(ωx+φ)的图象变换规律,余弦函数的定义域和值域,属于中档题.

| A. | ${x^2}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}-{y^2}=1$ | C. | $\frac{y^2}{4}-{x^2}=1$ | D. | ${y^2}-\frac{x^2}{4}=1$ |
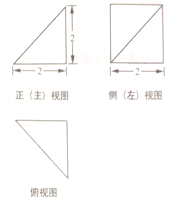
| A. | $8+4\sqrt{2}$ | B. | $6+\sqrt{2}+2\sqrt{3}$ | C. | $6+4\sqrt{2}$ | D. | $6+2\sqrt{2}+2\sqrt{3}$ |
 已知具有相关关系的两个变量x,y之间的几组数据如下表所示:
已知具有相关关系的两个变量x,y之间的几组数据如下表所示:| x | 2 | 4 | 6 | 8 | 10 |
| y | 3 | 6 | 7 | 10 | 12 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并估计当x=20时,y的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线2x-y-4=0的右下方的概率.
参考公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.