题目内容
若点（2a，a-1）在圆x2+（y-1）2=5的内部，则a的取值范围是 ．
考点：点与圆的位置关系
专题：计算题,直线与圆
分析：根据点（2a，a-1）在圆x2+（y-1）2=5的内部，可得不等式4a2+（a-2）2＜5，解之即可求得a的取值范围
解答：
解：由题意，4a2+（a-2）2＜5
即5a2-4a-1＜0
解之得：-
＜a＜1．
故答案为：-
＜a＜1．
即5a2-4a-1＜0
解之得：-
| 1 |
| 5 |
故答案为：-
| 1 |
| 5 |
点评：本题的考点是点与圆的位置关系，关键是由条件建立不等式，属于基础题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
若
（2x+
）dx=3+ln2，且a＞1，则a 的值为（ ）
| ∫ | a 1 |
| 1 |
| x |
| A、6 | B、4 | C、3 | D、2 |
如题图所示为某空间几何体的三视图，则该几何体的表面积为（ ）
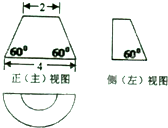
A、
| ||||
B、
| ||||
C、
| ||||
D、
|