题目内容
已知tanα=3,求下列各式的值:
(1)
;
(2)2sin2α-3sinαcosα;
(3)
.
(1)
| ||
|
(2)2sin2α-3sinαcosα;
(3)
| 5sin3α+cosα |
| 2cos3α+sin2αcosα |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)原式分子分母除以cosα,利用同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值;
(2)原式分母看做“1”,利用同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值;
(3)原式分子分母除以cos3α,利用同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值.
(2)原式分母看做“1”,利用同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值;
(3)原式分子分母除以cos3α,利用同角三角函数间的基本关系化简,把tanα的值代入计算即可求出值.
解答:
解:(1)∵tanα=3,
∴原式=
=
=
=-2+
;
(2)∵tanα=3,
∴原式=
=
=
=
;
(3)∵tanα=3,
∴cos2α=
=
,
则原式=
=
=
.
∴原式=
| ||
|
| ||
|
12-6
| ||
| -6 |
| 3 |
(2)∵tanα=3,
∴原式=
| 2sin2α-3sinαcosα |
| sin2α+cos2α |
| 2tan2α-3tanα |
| tan2α+1 |
| 18-9 |
| 9+1 |
| 9 |
| 10 |
(3)∵tanα=3,
∴cos2α=
| 1 |
| 1+tan2α |
| 1 |
| 10 |
则原式=
5tan3α+
| ||
| 2+tan2α |
| 5×27+10 |
| 2+9 |
| 145 |
| 11 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
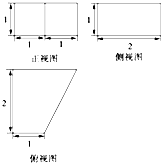
 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.
如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.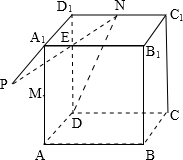 如图,在一封闭的正方体容器内装满水,M、N分别是AA1与C1D1的中点,由于某种原因,在D、M、N三点处各有一个小洞,为此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?
如图,在一封闭的正方体容器内装满水,M、N分别是AA1与C1D1的中点,由于某种原因,在D、M、N三点处各有一个小洞,为此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?