题目内容
已知道函数f(x)=alnx+
x2+(a+1)x+3
(1)当a=-1时,求函数f(x)的单调递减区间.
(2)若函数f(x)在区间(0,+∞)上是增函数,求实数a的取值范围.
| 1 |
| 2 |
(1)当a=-1时,求函数f(x)的单调递减区间.
(2)若函数f(x)在区间(0,+∞)上是增函数,求实数a的取值范围.
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)a=-1时,f(x)=-lnx+
x2+3,得f′(x)=x-
,令f′(x)<0,解得:0<x<1,从而f(x)在(0,1)递减;
(2)由f′(x)=
+x+a+1,(x>0),令f′(x)≥0,即
+x+a+1≥0,从而求出a≥0.
| 1 |
| 2 |
| 1 |
| x |
(2)由f′(x)=
| a |
| x |
| a |
| x |
解答:
解:(1)a=-1时,f(x)=-lnx+
x2+3,
∴f′(x)=x-
,
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减;
(2)∵f′(x)=
+x+a+1,(x>0),
令f′(x)≥0,即
+x+a+1≥0,
整理得:a(1+x)≥-x(1+x),
∴a≥0.
| 1 |
| 2 |
∴f′(x)=x-
| 1 |
| x |
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减;
(2)∵f′(x)=
| a |
| x |
令f′(x)≥0,即
| a |
| x |
整理得:a(1+x)≥-x(1+x),
∴a≥0.
点评:本题考察了函数的单调性,导数的应用,求参数的范围,是一道基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
设F是椭圆
+y2=1的一个焦点,则椭圆上与点F的距离等于长半轴长点的坐标是( )
| x2 |
| 4 |
| A、(0,±2) | ||||
| B、(0,±1) | ||||
C、(
| ||||
D、(0,±
|
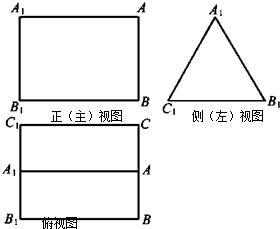 如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.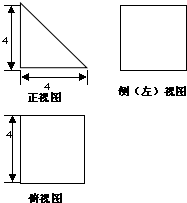 如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.
如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.