题目内容
数列{an}的前n项和Sn=n2-4n,则|a1|+|a2|+…+|a10|= .
考点:数列的求和
专题:等差数列与等比数列
分析:由数列{an}的前n项和Sn=n2-4n,能求出an=2n-5,从而得到|a1|+|a2|+…+|a10|=S10-2S2.
解答:
解:∵数列{an}的前n项和Sn=n2-4n,
∴a1=S1=1-4=-3,
n≥2时,an=Sn-Sn-1
=(n2-4n)-[(n-1)2-4(n-1)]
=2n-5,
n=1时,成立,
∴an=2n-5,
由an=2n-5≥0,得n≥
,
∴|a1|+|a2|+…+|a10|
=S10-2S2
=(100-40)-2(4-8)
=68.
故答案为:68.
∴a1=S1=1-4=-3,
n≥2时,an=Sn-Sn-1
=(n2-4n)-[(n-1)2-4(n-1)]
=2n-5,
n=1时,成立,
∴an=2n-5,
由an=2n-5≥0,得n≥
| 5 |
| 2 |
∴|a1|+|a2|+…+|a10|
=S10-2S2
=(100-40)-2(4-8)
=68.
故答案为:68.
点评:本题考查数列的前10项和的求法,是中档题,解题时要认真审题,注意公式n≥2时,an=Sn-Sn-1的合理运用.

练习册系列答案
相关题目
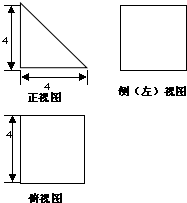 如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.
如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.