题目内容
19.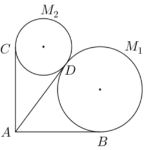 某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;
某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;(1)若∠BAD=60°,求圆M1、M2的半径(结果精确到0.1米)
(2)若观景步道M1与M2的造价分别为每米0.8千元与每米0.9千元,如何设计圆M1、M2的大小,使总造价最低?最低总造价是多少?(结果精确到0.1千元)
分析 (1)直接利用三角函数,可得结论;
(2)设∠BAD=2α,则总造价y=0.8•2π•60tanα+0.9•2π•60tan(45°-α),换元,利用基本不等式,可得结论.
解答 解:(1)M1半径=60tan30°≈34.6,M2半径=60tan15°≈16.1;
(2)设∠BAD=2α,则总造价y=0.8•2π•60tanα+0.9•2π•60tan(45°-α),
设1+tanα=x,则y=12π•(8x+$\frac{18}{x}$-17)≥84π,当且仅当x=$\frac{3}{2}$,tanα=$\frac{1}{2}$时,取等号,
∴M1半径30,M2半径20,造价263.8千元.
点评 本题考查直线与圆的位置关系,考查基本不等式的运用,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.设实数x,y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x-1≥0}\end{array}\right.$,则目标函数$z=\frac{y}{x+1}$的取值范围是( )
| A. | $(-∞,-\frac{1}{2}]∪[{0,\frac{3}{2}}]$ | B. | $[{\frac{1}{4},\frac{3}{2}}]$ | C. | $[{-\frac{1}{2},\frac{1}{4}}]$ | D. | $[{-\frac{1}{2},\frac{3}{2}}]$ |
14.函数f(x)=(x-1)2的单调递增区间是( )
| A. | [0,+∞) | B. | [1,+∞) | C. | (-∞,0] | D. | (-∞,1] |
8.已知集合A={x|x2-2x-3≤0},B={y|y=2x},则A∩B=( )
| A. | (0,3] | B. | (0,3) | C. | [0,3] | D. | [3,+∞) |