题目内容
9.已知幂函数f(x)=x${\;}^{({m}^{2}+m)^{-1}}$(m∈N*)的图象经过点$({2,\sqrt{2}})$.(1)试求m的值并写出该幂函数的解析式;
(2)试求满足f(1+a)>f(3-$\sqrt{a}}$)的实数a的取值范围.
分析 (1)根据幂函数的定义,把点的坐标代入函数解析式,求出m的值,从而求出函数的解析式即可;
(2)根据函数的单调性得到关于a的不等式,解出即可.
解答 解:(1)∵幂函数f(x)的图象经过点$({2,\sqrt{2}})$,
∴$\sqrt{2}$=${2}^{{{(m}^{2}+m)}^{-1}}$,即m2+m=2,解得:m=1或m=-2,
∵m∈N*,故m=1,
故f(x)=$\sqrt{x}$,x∈[0,+∞);
(2)∵f(x)在[0,+∞)递增,
由f(1+a)>f(3-$\sqrt{a}}$),
得$\left\{\begin{array}{l}{1+a≥0}\\{3-\sqrt{a}≥0}\\{1+a>3-\sqrt{a}}\end{array}\right.$,解得:1<a≤9,
故a的范围是(1,9].
点评 本题考查了幂函数的定义,考查函数的单调性问题,是一道基础题.

练习册系列答案
相关题目
18.已知直线y=2x-3与抛物线y2=4x交于A,B两点,O为坐标原点,OA,OB的斜率分别为k1,k2,则$\frac{1}{k_1}+\frac{1}{k_2}$( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{3}$ |
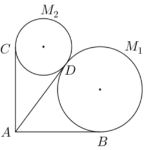 某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;
某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;