题目内容

7．若等差数列{an}的前5项的和为25，则a1+a5=10．

分析 由等差数列前n项和公式得${S}_{5}=\frac{5}{2}（{a}_{1}+{a}_{5}）$=25，由此能求出a1+a5．

解答 解：∵等差数列{an}的前5项的和为25，
∴${S}_{5}=\frac{5}{2}（{a}_{1}+{a}_{5}）$=25，
∴a1+a5=25×$\frac{2}{5}$=10．
故答案为：10．

点评 本题考查等差数列中两项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
17．已知函数$f（x）=sin（{x+\frac{π}{2}}）cos（{x-\frac{π}{3}}）$．
（1）求函数f（x）的最小正周期；
（2）将函数y=f（x）的图象向下平移$\frac{1}{4}$个单位，再将图象上各点的纵坐标伸长为原来的4倍（横坐标不变），得到函数y=g（x）的图象，求函数y=g（x）在$[{0，\frac{π}{3}}]$上的最大值．
18．已知直线y=2x-3与抛物线y2=4x交于A，B两点，O为坐标原点，OA，OB的斜率分别为k1，k2，则$\frac{1}{k_1}+\frac{1}{k_2}$（　　）
A．$\frac{1}{2}$B．2C．$-\frac{1}{2}$D．$-\frac{1}{3}$
15．设f（x）=|x-1|+2|x+1|的最小值为m．
（Ⅰ）求m的值；
（Ⅱ）设a，b∈R，a2+b2=m，求$\frac{1}{{a}^{2}+1}+\frac{4}{{b}^{2}+1}$的最小值．
2．设集合A={1，2，3}，集合B={3，4}，则A∪B={1，2，3，4}．
12．设a1、a2、…、a6为1、2、3、4、5、6的一个排列，则满足|a1-a2|+|a3-a4|+|a5-a6|=3的不同排列的个数为48．
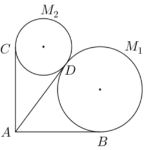19．某景区欲建造两条圆形观景步道M1、M2（宽度忽略不计），如图所示，已知AB⊥AC，AB=AC=AD=60（单位：米），要求圆M1与AB、AD分别相切于点B、D，圆M2与AC、AD分别相切于点C、D；
（1）若∠BAD=60°，求圆M1、M2的半径（结果精确到0.1米）
（2）若观景步道M1与M2的造价分别为每米0.8千元与每米0.9千元，如何设计圆M1、M2的大小，使总造价最低？最低总造价是多少？（结果精确到0.1千元）
16．已知集合A={x∈N|x-2≤0}，集合B={x|x2-x-2＜0}，则A∩B=（　　）
A．{1，2}B．{0，1}C．{0，1，2}D．{-1，0，1，2}
17．已知数列{an}的通项公式为an=2n-（-1）n，n∈N*．
（1）在数列{an}中，是否存在连续3项成等差数列？若存在，求出所有符合条件的项，若不存在，说明理由；
（2）试证在数列{an}中，一定存在满足条件1＜r＜s的正整数r、s，使得a1、ar、as成等差数列；并求出正整数r、s之间的关系；
（3）在数列{an}中是否存在某4项成等差数列？若存在，求出所有满足条件的项；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网