题目内容
10.设实数x,y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x-1≥0}\end{array}\right.$,则目标函数$z=\frac{y}{x+1}$的取值范围是( )| A. | $(-∞,-\frac{1}{2}]∪[{0,\frac{3}{2}}]$ | B. | $[{\frac{1}{4},\frac{3}{2}}]$ | C. | $[{-\frac{1}{2},\frac{1}{4}}]$ | D. | $[{-\frac{1}{2},\frac{3}{2}}]$ |
分析 由约束条件作出可行域,再由目标函数$z=\frac{y}{x+1}$的几何意义,即可行域内的点与定点(-1,0)连线的斜率求解.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x-1≥0}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x=1}\\{x-y=2}\end{array}\right.$,得A(1,-1),
联立$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,得B(1,3).
由$z=\frac{y}{x+1}$=$\frac{y-0}{x-(-1)}$,而${k}_{PA}=-\frac{1}{2},{k}_{PB}=\frac{3}{2}$.
∴目标函数$z=\frac{y}{x+1}$的取值范围是[$-\frac{1}{2}$,$\frac{3}{2}$].
故选:D.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
相关题目
18.已知直线y=2x-3与抛物线y2=4x交于A,B两点,O为坐标原点,OA,OB的斜率分别为k1,k2,则$\frac{1}{k_1}+\frac{1}{k_2}$( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{3}$ |
5.已知复数z满足(z+i)(1-2i)=2,则复数z在复平面内的对应点所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
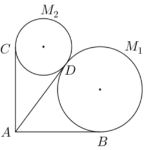 某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;
某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;