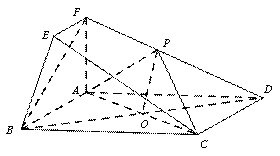
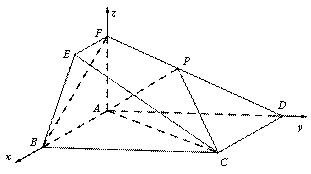
题目内容
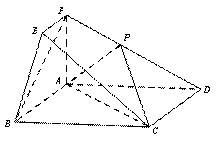
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD, EF // AB,
∠BAF=90º, AD= 2,AB=AF=2EF =1,点P在棱DF上.
(Ⅰ)若P是DF的中点
(ⅰ) 求证:BF // 平面ACP
(ⅱ) 求异面直线BE与CP所成角的余弦值
(Ⅱ)若二面角D-AP-C的余弦值为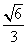 ,求PF的长度.
,求PF的长度.
Ⅰ)(ⅰ)证明:连接BD,交AC于点O,连接OP.
因为P是DF中点,O为矩形ABCD 对角线的交点,
所以OP为三角形BDF中位线,
所以BF // OP,
因为BF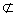 平面ACP,OP
平面ACP,OP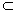 平面ACP,
平面ACP,
 所以BF // 平面ACP.
所以BF // 平面ACP.
(ⅱ)因为∠BAF=90º,
所以AF⊥AB,
因为 平面ABEF⊥平面ABCD,
且平面ABEF ∩平面ABCD= AB,
所以AF⊥平面ABCD,
因为四边形ABCD为矩形,
所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系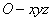 .
.
所以 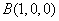 ,
,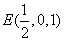 ,
, ,
,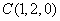 .
.
所以 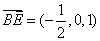 ,
,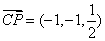 ,
,
 所以
所以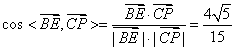 ,
,
即异面直线BE与CP所成角的余弦值为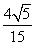 .
.
(Ⅱ)解:因为AB⊥平面ADF,
所以平面APF的法向量为 .
.
设P点坐标为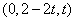 ,
,
在平面APC中,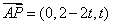 ,
,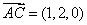 ,
,
所以 平面APC的法向量为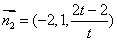 ,
,
所以 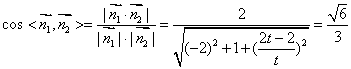 ,
,
解得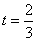 ,或
,或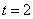 (舍).
(舍).
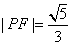 .
.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 中,
中,  ,则一只小虫从A点沿长方体的表面爬到
,则一只小虫从A点沿长方体的表面爬到 点的最短距离是 。
点的最短距离是 。  >0,函数
>0,函数 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 ,点
,点 在
在 所表示的平面区域内, 则
所表示的平面区域内, 则 在
在
 B.
B. 
 D.
D. 
 中,三个内角
中,三个内角 的对边分别为
的对边分别为 ,且满足
,且满足 ,则
,则 的最大值为________
的最大值为________ ,
, ,
, ,则 ( )
,则 ( ) B
B  C
C  D
D 
 恰有两个解,则实数
恰有两个解,则实数 的取值集合为 ( )
的取值集合为 ( ) B.
B.  C.
C.  D.
D. 


 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系数是 ( )
的系数是 ( )