题目内容
9.若点P(1,-2)位于角α终边上,则sin2α+2cos2α=( )| A. | -$\frac{14}{5}$ | B. | -$\frac{7}{5}$ | C. | -2 | D. | $\frac{4}{5}$ |
分析 利用点P(1,-2)位于角α终边上,求得tanα的值,进而利用万能公式对sin2α+2cos2α化简整理后,把tanα的值代入即可.
解答 解:∵点P(1,-2)位于角α终边上,
∴tanα=-2.
∴sin2α+2cos2α=$\frac{2tanα}{1+ta{n}^{2}α}$+2•$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=-2.
故选C.
点评 本题主要考查了同角三角函数基本关系的运用,万能公式的应用.要熟练记忆同角三角函数中的平方关系,倒数关系及商数关系等.

练习册系列答案
相关题目
17.如图所示,在△ABC中,M在BC上,N在AM上,CM=CN,且$\frac{AM}{AN}$=$\frac{BM}{CN}$,下列结论中正确的是( )
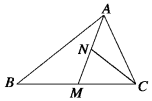

| A. | △ABM∽△ACB | B. | △ANC∽△AMB | C. | △ANC∽△ACM | D. | △CMN∽△BCA |
4.如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是( )
| A. | 0 | B. | 0 或1 | C. | 1 | D. | 0 或1或-1 |
8.已知tanα=2则cos($\frac{2015π}{2}$-2α)的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | 2 | D. | $-\frac{1}{2}$ |