题目内容
12.计算:$\frac{1}{2}{log_2}3\frac{1}{2}{log_9}8$=$\frac{3}{8}$.分析 利用导数换底公式化简求解即可.
解答 解:$\frac{1}{2}{log_2}3\frac{1}{2}{log_9}8$=$\frac{1}{2}•\frac{lg3}{lg2}•\frac{1}{2}•\frac{lg8}{lg9}$=$\frac{1}{4}•\frac{lg3}{lg2}•\frac{3lg2}{2lg3}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查了对数换底公式的应用以及对数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
17.如图所示,在△ABC中,M在BC上,N在AM上,CM=CN,且$\frac{AM}{AN}$=$\frac{BM}{CN}$,下列结论中正确的是( )
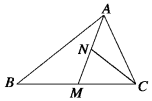

| A. | △ABM∽△ACB | B. | △ANC∽△AMB | C. | △ANC∽△ACM | D. | △CMN∽△BCA |
4.如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是( )
| A. | 0 | B. | 0 或1 | C. | 1 | D. | 0 或1或-1 |
 如图,圆A:(x+1)2+y2=16,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
如图,圆A:(x+1)2+y2=16,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E. 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.