题目内容
4.如图是函数y=f(x)图象的一部分,则函数y=f(x)的解析式可能为( )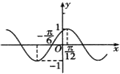
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=cos(4x-$\frac{π}{3}$) | D. | y=cos(2x-$\frac{π}{6}$) |
分析 由函数的最大值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:根据函数y=f(x)图象的一部分,可设f(x)=sin(ωx+φ),由$\frac{1}{4}•\frac{2π}{ω}$=$\frac{π}{12}$+$\frac{π}{6}$,可得ω=2,
再根据五点法作图可得2×$\frac{π}{12}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{3}$,故f(x)=sin(2x+$\frac{π}{3}$)=cos(2x-$\frac{π}{6}$),
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最大值求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
15.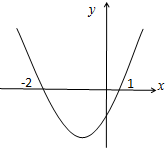 若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
 若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(-2),无极小值 | B. | 函数f(x)有极大值f(1),无极小值 | ||
| C. | 函数f(x)有极大值f(-2)和极小值f(1) | D. | 函数f(x)有极大值f(1)和极小值f(-2). |
9.若不等式$\frac{4x+1}{x+2}$<0和不等式ax2+bx-2>0的解集相同,则a、b的值为( )
| A. | a=-8,b=-10 | B. | a=-4,b=-9 | C. | a=-1,b=9 | D. | a=-1,b=2 |
16.已知圆(x-1)2+(y-1)2=4上到直线y=x+b的距离等于1的点有且仅有2个,则b的取值范围是( )
| A. | (-$\sqrt{2}$,0)U(0,$\sqrt{2}$) | B. | (-3$\sqrt{2}$,3$\sqrt{2}$) | C. | (-3$\sqrt{2}$,-$\sqrt{2}$)U($\sqrt{2}$,3$\sqrt{2}$) | D. | (-3$\sqrt{2}$,-$\sqrt{2}$]U($\sqrt{2}$,3$\sqrt{2}$) |
13.若正数x,y满足4x+y-1=0,则$\frac{x+y}{xy}$的最小值为( )
| A. | 12 | B. | 10 | C. | 9 | D. | 8 |