题目内容
14.在△ABC中,已知内角A=$\frac{π}{3}$,边BC=2$\sqrt{3}$.设内角B=x,面积为y.(Ⅰ)求函数y=f(x)的解析式和定义域;
(Ⅱ)求y的最大值.
分析 (I)由已知角A及三角形的内角和定理可求x的范围,然后由正弦定理,$AC=\frac{BC}{sinA}sinB=4sinx$,代入三角形的面积公式,即可求解;
(II)利用两角差的正弦公式及辅助角公式对(I)中的函数关系进行化简,结合正弦函数的性质即可求解取得最大值时的x即B及相应的最大值.
解答 解:(Ⅰ)△ABC的内角和A+B+C=π
∵$A=\frac{π}{3}$
∴$0<B<\frac{2π}{3}$…(1分)
∵$AC=\frac{BC}{sinA}sinB=4sinx$…(4分)
y=$\frac{1}{2}$AB•ACsinA=4$\sqrt{3}$ sinxsin($\frac{2π}{3}$-x)(0<x<$\frac{2π}{3}$)…(6分)
(II)y=4$\sqrt{3}$sinxsin($\frac{2π}{3}$-x)=4$\sqrt{3}$sinx($\frac{\sqrt{3}}{2}$cosx+$\frac{1}{2}$sinx)
=6sinxcosx+2$\sqrt{3}$sin2x
=3sin2x+$\sqrt{3}$-$\sqrt{3}$cos2x=2$\sqrt{3}$sin(2x-$\frac{π}{6}$)+$\sqrt{3}$(-$\frac{π}{6}$<2x-$\frac{π}{6}$<$\frac{7π}{6}$)…(8分)
当2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$时,y取得最大值3$\sqrt{3}$
∴B=$\frac{π}{3}$时,△ABC的面积最大为3$\sqrt{3}$…(12分)
点评 本题综合考查了三角形的正弦定理、内角和定理及两角差的正弦公式、辅助角公式及正弦函数的性质等知识的综合应用

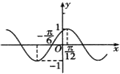
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=cos(4x-$\frac{π}{3}$) | D. | y=cos(2x-$\frac{π}{6}$) |
| A. | p?Q | B. | P∩Q=∅ | C. | P∪Q=Q | D. | CRP=Q |
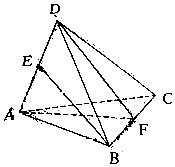 如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.