题目内容
9．若不等式$\frac{4x+1}{x+2}$＜0和不等式ax2+bx-2＞0的解集相同，则a、b的值为（ ）| A． | a=-8，b=-10 | B． | a=-4，b=-9 | C． | a=-1，b=9 | D． | a=-1，b=2 |
分析 分别求解不等式$\frac{4x+1}{x+2}$＜0和不等式ax2+bx-2＞0的解集，它们解集相同，可求a、b的值．
解答 解：不等式$\frac{4x+1}{x+2}$＜0等价于（4x+1）（x+2）＜0，
解得：$-2＜x＜-\frac{1}{4}$，
∵解集相同，
∴不等式ax2+bx-2＞0的解集为$-2＜x＜-\frac{1}{4}$，
由方程与不等式的关系可知：ax2+bx-2=0的根为：${x}_{1}=-2，{x}_{2}=-\frac{1}{4}$，
由韦达定理：$\left\{\begin{array}{l}{{x}_{1}{x}_{2}=-\frac{2}{a}}\\{{x}_{1}+{x}_{2}=-\frac{b}{a}}\end{array}\right.$，解得：a=-4，b=-9，
故选：B．
点评 本题考察了分式不等式的解法和方程与不等式的关系，属于基础题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
20．若直线x+y-1=0与抛物线y=2x2交于A，B两点，则点M（1，0）到A，B两点的距离之积为（ ）
| A． | $4\sqrt{2}$ | B． | $2\sqrt{2}$ | C． | 4 | D． | 2 |
4．如图是函数y=f（x）图象的一部分，则函数y=f（x）的解析式可能为（ ）
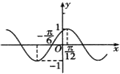
| A． | y=sin（x+$\frac{π}{6}$） | B． | y=sin（2x-$\frac{π}{6}$） | C． | y=cos（4x-$\frac{π}{3}$） | D． | y=cos（2x-$\frac{π}{6}$） |
14．已知双曲线的中心为原点，离心率e=$\sqrt{5}$，且它的一个焦点与抛物线x2=-8$\sqrt{5}$y的焦点重合，则此双曲线方程为（ ）
| A． | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B． | $\frac{y^2}{4}-\frac{x^2}{16}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{16}=1$ |
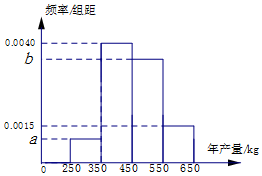某人种植一种经济作物，根据以往的年产量数据，得到年产量频率分布直方图如图所示，以各区间中点值作为该区间的年产量，得到平均年产量为455kg，已知当年产量低于350kg时，单位售价为20元/kg，若当年产量不低于350kg而低于550时，单位售价为15元/kg，当年产量不低于550kg时，单位售价为10元/kg．
18．在△ABC中，根据下列条件解三角形，则其中有两个解的是（ ）
| A． | a=80，b=61，A=60° | B． | a=10，b=14，A=30° | ||
| C． | b=23，A=45°，B=30° | D． | a=61，c=47，A=120° |