题目内容
函数y=tan(
x-
)的定义域是 .
| 1 |
| 2 |
| π |
| 4 |
考点:正切函数的定义域
专题:三角函数的图像与性质
分析:由
x-
≠kπ+
解不等式可得函数的定义域.
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
解答:
解:由
x-
≠kπ+
可解得x≠2kπ+
,k∈Z,
∴函数y=tan(
x-
)的定义域为{x|x≠2kπ+
,k∈Z},
故答案为:{x|x≠2kπ+
,k∈Z}
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
∴函数y=tan(
| 1 |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
故答案为:{x|x≠2kπ+
| 3π |
| 2 |
点评:本题考查正切函数的定义域,属基础题.

练习册系列答案
相关题目
若书架上放有的数学,物理,化学书分别是5本,3本,2本,则随机抽出一本是物理书的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若 x>0,y>0,且x+y=s,xy=p,则下列命题中正确的是( )
A、当且仅当x=y时s有最小值2
| ||
B、当且仅当x=y时p有最大值
| ||
C、当且仅当p为定值时s有最小值2
| ||
D、若s为定值,当且仅当x=y时p有最大值
|
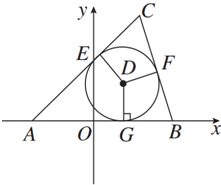 △ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是
△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是