题目内容
10.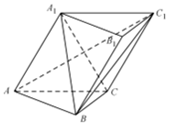 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.(1)求证:平面A1BC⊥平面ABC1;
(2)若直线AA1与底面ABC所成的角为60°,求直线AA1与平面ABC1所成角的正弦值.
分析 (1)推导出BC⊥侧面ACC1A1,所以AC1⊥BC,再由A1B⊥AC1,得到AC1⊥面A1BC,由此能证明面ABC1⊥面A1BC.
(2)利用等体积方法,求出A1到平面ABC1的距离,即可求直线AA1与平面ABC1所成角的正弦值.
解答 (1)证明:因为底面ABC是等腰直角三角形,CA=CB,所以BC⊥AC
因为侧面ACC1A1⊥底面ABC,侧面ACC1A1∩底面ABC=AC,
所以BC⊥侧面ACC1A1,所以AC1⊥BC,
又A1B⊥AC1,而A1B∩BC=B,
所以AC1⊥面A1BC,
又AC1?面ABC1,所以面ABC1⊥面A1BC;
(2)解:由题意,∠A1AC=60°,四边形ACC1A1是菱形.
设AC=2,则AB=2$\sqrt{2}$,AC1=2$\sqrt{3}$,BC1=2$\sqrt{2}$,∴${S}_{△AB{C}_{1}}$=$\frac{1}{2}×2\sqrt{2}×\sqrt{8-3}$=$\sqrt{10}$
设A1到平面ABC1的距离为h,则$\frac{1}{3}×\sqrt{10}×h$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{3}×1×2$,
∴h=$\frac{\sqrt{30}}{5}$,
∴直线AA1与平面ABC1所成角的正弦值=$\frac{\frac{\sqrt{30}}{5}}{2}$=$\frac{\sqrt{30}}{10}$.
点评 本题考查线面垂直、面面垂直的证明,考查线面角,考查学生的计算能力,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
1.若将函数f(x)=1+sinωx(0<ω<4,ω∈Z)的图象向右平移$\frac{π}{3}$个单位后,得到函数y=g(x)的图象,且y=g(x)的图象的一条对称轴方程为x=$\frac{π}{2}$,则分f(x)的最小正周期为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
5.若($\frac{1}{2}$x-2y)2n+1的展开式中前n+1项的二项式系数之和为64,则该展开式中x4y3的系数是( )
| A. | -$\frac{35}{2}$ | B. | 70 | C. | $\frac{35}{2}$ | D. | -70 |
2.将数字“124467”重新排列后得到不同的偶数个数为( )
| A. | 72 | B. | 120 | C. | 192 | D. | 240 |
19.已知集合A={x|0<x≤3,x∈N},B={x|y=$\sqrt{{x}^{2}-9}$},则集合A∩(∁RB)=( )
| A. | {1,2} | B. | {1,2,3} | C. | {0,1,2} | D. | (0,1) |
20.某校在高一年级学生中,对自然科学类、社会科学类校本选修课程的选课意向进行调查.现从高一年级学生中随机抽取180名学生,其中男生105名;在这名180学生中选择社会科学类的男生、女生均为45名.
(1)试问:从高一年级学生中随机抽取1人,抽到男生的概率约为多少?
(2)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
附:${K^2}=\frac{{n{{({ab-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
(1)试问:从高一年级学生中随机抽取1人,抽到男生的概率约为多少?
(2)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
| 选择自然科学类 | 选择社会科学类 | 合计 | |
| 男生 | 60 | 45 | 105 |
| 女生 | 30 | 45 | 75 |
| 合计 | 90 | 90 | 180 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |