题目内容
5.若($\frac{1}{2}$x-2y)2n+1的展开式中前n+1项的二项式系数之和为64,则该展开式中x4y3的系数是( )| A. | -$\frac{35}{2}$ | B. | 70 | C. | $\frac{35}{2}$ | D. | -70 |
分析 根据($\frac{1}{2}$x-2y)2n+1展开式中前n+1项的二项式系数之和等于后n+1项的和,
求出n的值,再利用展开式的通项公式求出x4y3的系数.
解答 解:($\frac{1}{2}$x-2y)2n+1展开式中共有2n+2项,
其前n+1项的二项式系数之和等于后n+1项和,
∴22n+1=64×2,解得n=3;
∴($\frac{1}{2}$x-2y)7展开式中通项公式为
Tr+1=${C}_{7}^{r}$•${(\frac{1}{2}x)}^{7-r}$•(-2y)r,
令r=3,得展开式中x4y3的系数是
${C}_{7}^{3}$•${(\frac{1}{2})}^{4}$•(-2)3=-$\frac{35}{2}$.
故选:A.
点评 本题考查了二项式展开式的通项公式与二项式系数的应用问题,是基础题.

练习册系列答案
相关题目
16.已知曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1右焦点为F,P为双曲线左支点上一点,点A(0,$\sqrt{2}$),则△APF周长的最小值为( )
| A. | 4(1+$\sqrt{2}$) | B. | 4+$\sqrt{2}$ | C. | 2($\sqrt{2}$+$\sqrt{6}$) | D. | $\sqrt{6}$+3$\sqrt{2}$ |
13.设函数f(x)的定义域为R,f(x)=$\left\{{\begin{array}{l}{x,0≤x<1}\\{{{(\frac{1}{3})}^x}-1,-1≤x<0}\end{array}}$且对任意的x∈R都有f(x+1)=f(x-1),若在区间[-1,5)上函数g(x)=f(x)-mx-m恰有4个不同零点,则实数m的取值范围是( )
| A. | $({0,\frac{1}{4}}]$ | B. | $({\frac{1}{4},\frac{1}{2}}]$ | C. | $[{\frac{1}{4},\frac{1}{2}})$ | D. | $({0,\frac{1}{2}})$ |
17.要计算1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2017}$的结果,如图程序框图中的判断框内可以填( )

| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴长为2,离心率为$\sqrt{5}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{16}$=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{2}$$-\frac{{y}^{2}}{3}$=1 | D. | x2$-\frac{{y}^{2}}{6}$=1 |
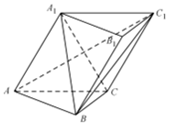 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.