题目内容
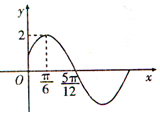
1.若将函数f(x)=1+sinωx(0<ω<4,ω∈Z)的图象向右平移$\frac{π}{3}$个单位后,得到函数y=g(x)的图象,且y=g(x)的图象的一条对称轴方程为x=$\frac{π}{2}$,则分f(x)的最小正周期为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数图象的对称性,求得ω的值,进而利用正弦函数的周期公式即可计算得解.
解答 解:将函数f(x)=1+sinωx的图象向右平移$\frac{π}{3}$个单位后,
得到的图象对应的解析式为:y=g(x)=sin[ω(x-$\frac{π}{3}$)]+1=sin(ωx-$\frac{ωπ}{3}$)+1,
∵y=g(x)的图象的一条对称轴方程为x=$\frac{π}{2}$,
∴$\frac{π}{2}$ω-$\frac{ωπ}{3}$=kπ+$\frac{π}{2}$,k∈Z,解得:ω=6k+3,k∈Z,
∵0<ω<4,
∴ω=3,可得:f(x)=1+sin3x,
∴f(x)的最小正周期为T=$\frac{2π}{3}$.
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数图象的对称性,三角函数周期公式的应用,考查了数形结合思想,属于基础题.

练习册系列答案
相关题目
16.已知曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1右焦点为F,P为双曲线左支点上一点,点A(0,$\sqrt{2}$),则△APF周长的最小值为( )
| A. | 4(1+$\sqrt{2}$) | B. | 4+$\sqrt{2}$ | C. | 2($\sqrt{2}$+$\sqrt{6}$) | D. | $\sqrt{6}$+3$\sqrt{2}$ |
13.设函数f(x)的定义域为R,f(x)=$\left\{{\begin{array}{l}{x,0≤x<1}\\{{{(\frac{1}{3})}^x}-1,-1≤x<0}\end{array}}$且对任意的x∈R都有f(x+1)=f(x-1),若在区间[-1,5)上函数g(x)=f(x)-mx-m恰有4个不同零点,则实数m的取值范围是( )
| A. | $({0,\frac{1}{4}}]$ | B. | $({\frac{1}{4},\frac{1}{2}}]$ | C. | $[{\frac{1}{4},\frac{1}{2}})$ | D. | $({0,\frac{1}{2}})$ |
11.执行如图所示的程序框图,若输入的a,b分别为36,28,则输出的a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 20 |
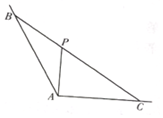 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.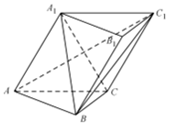 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.