题目内容
15.在推理“因为y=sinx在[0,$\frac{π}{2}$]上是增函数,所以sin$\frac{3π}{7}$>sin$\frac{2π}{5}$”中,大前提是y=sinx在[0,$\frac{π}{2}$]上是增函数;小前提是$\frac{3π}{7}$>$\frac{2π}{5}$且 $\frac{3π}{7}$,$\frac{2π}{5}$∈[0,$\frac{π}{2}$];结论是sin$\frac{3π}{7}$>sin$\frac{2π}{5}$.分析 由题意,根据三段论的形式“大前提,小前提,结论”直接写出答案即可
解答 解:用三段论的形式写出“因为y=sinx在[0,$\frac{π}{2}$]上是增函数,所以sin$\frac{3π}{7}$>sin$\frac{2π}{5}$”中,”的演绎推理是:
大前提 y=sinx在[0,$\frac{π}{2}$]上是增函数
小前提 $\frac{3π}{7}$>$\frac{2π}{5}$ 且 $\frac{3π}{7}$,$\frac{2π}{5}$∈[0,$\frac{π}{2}$]
结论 sin$\frac{3π}{7}$>sin$\frac{2π}{5}$
故答案为:y=sinx在[0,$\frac{π}{2}$]上是增函数,$\frac{3π}{7}$>$\frac{2π}{5}$ 且 $\frac{3π}{7}$,$\frac{2π}{5}$∈[0,$\frac{π}{2}$],sin$\frac{3π}{7}$>sin$\frac{2π}{5}$
点评 本题考查演绎推理--三段论,解题的关键是理解三段论的形式,本题是基础概念考查题.

练习册系列答案
相关题目
5.设M是△ABC边BC上的任意一点,$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{NM}$,若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
20.已知实数x,y满足$\left\{\begin{array}{l}{y≥x+2}\\{x+y≤6}\\{x≥1}\end{array}\right.$,则z=2|x-2|+|y|的最小值是( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
4.在△ABC中,AC=2AB=2,∠BAC=120°,O是BC的中点,M是AO上一点,且$\overrightarrow{AO}$=3$\overrightarrow{MO}$,则$\overrightarrow{MB}$$•\overrightarrow{MC}$的值是( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{7}{6}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{6}$ |
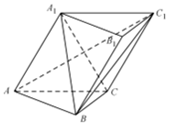 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.