题目内容

7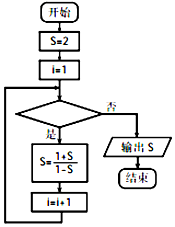．某程序框图如图所示，该程序运行后若输出S的值是2，则判断框内可填写（　　）
A．i≤2015？B．i≤2016？C．i≤2017？D．i≤2018？

分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算并输出S值．模拟程序的运行过程，用表格对程序运行过程中各变量的值进行分析，不难得到最终的输出结果．

解答 解：程序在运行过程中各变量的值如下表示：
          是否继续循环       S     i
循环前/2     1
第一圈      是-3    2
第二圈      是-$\frac{1}{2}$   3
第三圈      是               $\frac{1}{3}$    4
第四圈      是                2    5
第五圈      是-3   6
…
依此类推，S的值呈周期性变化：2，-3，-$\frac{1}{2}$，$\frac{1}{3}$，2，-3，…
第2016圈    是            $\frac{1}{3}$     2017
第2017圈    是            2    2018
故选C．

点评 本题考查循环结构的程序框图，解决本题的关键是弄清开始和结束循环的条件．

练习册系列答案
相关题目
1．已知两定点F1（-2，0），F2（2，0），曲线C上的动点M满足|MF1|+|MF2|=8，直线MF2与曲线C的另一个交点为P．
（Ⅰ）求曲线C的标准方程；
（Ⅱ）设点N（-4，0），若S${\;}_{△MN{F}_{2}}$：S${\;}_{△PN{F}_{2}}$=3：2，求直线MN的方程．
19．在△ABC中，D为三角形所在平面内一点，且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$，则$\frac{{{S_{△ABD}}}}{{{S_{△ABC}}}}$=（　　）
A．$\frac{2}{3}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{1}{2}$
15．平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$不共线，且两两所成的角相等，若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，|$\overrightarrow{c}$|=1，则|$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$|=1．
2．已知函数f（x）=|x-2|+2，g（x）=m|x|（m∈R）．
（Ⅰ）解关于x的不等式f（x）＞5；
（Ⅱ）若不等式f（x）≥g（x）对任意x∈R恒成立，求m的取值范围．
12．若直线ax-y-a+3=0将关于x，y的不等式组$\left\{\begin{array}{l}{x-2y+5≥0}\\{x+y-1≥0}\\{x-y+1≤0}\end{array}\right.$表示的平面区域分成面积相等的两部分，则z=4x-ay的最大值是4．
19．关于曲线C：x2+y4=1，给出下列四个命题：①曲线C有两条对称轴，一个对称中心；
②曲线C上的点到原点距离的最小值为1；③曲线C的长度l满足l＞4$\sqrt{2}$；④曲线C所围成图形的面积S满足π＜S＜4．
上述命题中，真命题的个数是（　　）
A．4B．3C．2D．1

已知集合，分别求适合下列条件的的值．

（1） ；

（2）．
5．已知双曲线C：$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{1}{2}$x，则双曲线C的离心率为（　　）
A．$\frac{\sqrt{5}}{2}$B．$\sqrt{5}$C．$\frac{\sqrt{6}}{2}$D．$\sqrt{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网