题目内容
2.已知函数f(x)=|x-2|+2,g(x)=m|x|(m∈R).(Ⅰ)解关于x的不等式f(x)>5;
(Ⅱ)若不等式f(x)≥g(x)对任意x∈R恒成立,求m的取值范围.
分析 (Ⅰ)由f(x)>5,得|x-2|>3,即可解关于x的不等式f(x)>5;
(Ⅱ)若不等式f(x)≥g(x)对任意x∈R恒成立,得|x-2|≥m|x|-2对任意x∈R恒成立,分类讨论,分离参数,即可求m的取值范围.
解答 解:(Ⅰ)由f(x)>5,得|x-2|>3,
即x-2<-3或x-2>3,…(3分)
∴x<-1或x>5.故原不等式的解集为{x|x<-1或x>5}…(5分)
(Ⅱ)由f(x)≥g(x),得|x-2|≥m|x|-2对任意x∈R恒成立,
当x=0时,不等式|x-2|≥m|x|-2成立,
当x≠0时,问题等价于$m≤\frac{{|{x-2}|+2}}{|x|}$对任意非零实数恒成立,…(7分)
∵$\frac{{|{x-2}|+2}}{|x|}≥\frac{{|{x-2+2}|}}{|x|}=1$,∴m≤1,即m的取值范围是(-∞,1].…(10分)
点评 本题考查不等式的解法,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.已知抛物线y2=4x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,则双曲线的离心率为( )
| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | 8$\sqrt{2}$-8 | D. | 2$\sqrt{2}$-2 |
10. 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )| A. | 6 | B. | 25 | C. | 100 | D. | 400 |
7.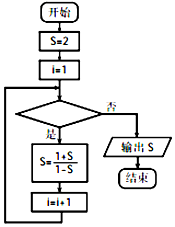 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )| A. | i≤2015? | B. | i≤2016? | C. | i≤2017? | D. | i≤2018? |
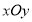 中,以原点
中,以原点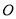 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线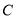 的极坐标方程为
的极坐标方程为 .
.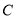 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;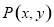 是曲线
是曲线 上的动点,求
上的动点,求 的取值范围.
的取值范围.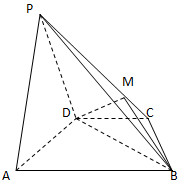 如图,在四棱锥P-ABCD中,AD=4,BD=8,平面PAD⊥平面ABCD,AB=2DC=4$\sqrt{5}$.
如图,在四棱锥P-ABCD中,AD=4,BD=8,平面PAD⊥平面ABCD,AB=2DC=4$\sqrt{5}$.