题目内容
9.设随机变量Z的分布列为若$E(Z)=\frac{15}{8}$,则x=$\frac{1}{8}$y=$\frac{3}{8}$| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
分析 利用离散型随机变量的分布列的概率和直接求解即可.
解答 解:∵离散型随机变量分布列的概率和为1,
∴0.5+x+y=1,且1×$0.5+2x+3y=\frac{15}{8}$
x=$\frac{1}{8}$.y=$\frac{3}{8}$.
故答案为:$\frac{1}{8}$,$\frac{3}{8}$.
点评 本题考查概率的求法,考查离散型概率分布列的性质的应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在五张牌中有三张K和两张A,如果不放回地一次抽取两张牌.记“第2次抽到扑克牌K的概率为x”,“在第一次抽到扑克牌K的条件下,第二次抽到扑克牌K的概率为y”,则实数x,y依次为( )
| A. | $\frac{3}{5}{,^{\;}}\frac{1}{2}$ | B. | $\frac{3}{5}{,^{\;}}\frac{3}{5}$ | C. | $\frac{1}{2}{,^{\;}}\frac{1}{2}$ | D. | $\frac{3}{5}{,^{\;}}\frac{2}{5}$ |
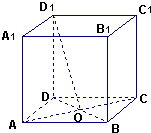 在正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,BD与AC交于点O,
在正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,BD与AC交于点O,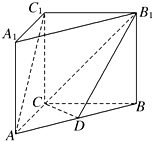 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.