题目内容
10.在△ABC中,角A、B、C的对边分别为a,b,c,∠B=60°且b=$\sqrt{3}$(Ⅰ)若a=1,求∠A的大小和边c的长度;
(Ⅱ)求△ABC周长的取值范围.
分析 (Ⅰ)由已知利用正弦定理可求sinA=$\frac{1}{2}$,结合范围$0<A<\frac{2π}{3}$,可求A的值,进而利用余弦定理可求c的值.
(Ⅱ)由正弦定理可求c=2sinC,a=2sinA,设周长为y,利用三角函数恒等变换的应用化简可得y=$2\sqrt{3}sin({A+\frac{π}{6}})+\sqrt{3}$,可求范围$\frac{π}{6}<A+\frac{π}{6}<\frac{5π}{6}$,利用正弦函数的性质可求取值范围.
解答 (本题满分12分)
解:(Ⅰ)$B=\frac{π}{3},A+C=\frac{2π}{3}$,
又∵$\frac{a}{sinA}=\frac{b}{sinB}$,a=1,$b=\sqrt{3}$,
∴$\frac{1}{sinA}=\frac{{\sqrt{3}}}{{\frac{{\sqrt{3}}}{2}}}$,
∴$sinA=\frac{1}{2}$,-----(2分)
又∵$0<A<\frac{2π}{3}$,-----(3分)(或用大边对大角),
∴$A=\frac{π}{6}$.-------(4分)
∴c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{{1}^{2}+3-2×1×\sqrt{3}×0}$=2.
(采用正弦定理,余弦定理,勾股定理均可)求出边长c的长度为2.-------------(6分)
(Ⅱ)∵$\frac{c}{sinC}=\frac{a}{sinA}=\frac{b}{sinB}=\frac{{\sqrt{3}}}{{\frac{{\sqrt{3}}}{2}}}=2$,
∴c=2sinC,a=2sinA,----(7分)
设周长为y,则$y=a+c+b=2sinA+2sinC+\sqrt{3}$
=$2sinA+2sin({\frac{2π}{3}-A})+\sqrt{3}$
=$3sinA+\sqrt{3}cosA+\sqrt{3}$,----(8分)
=$2\sqrt{3}({\frac{{\sqrt{3}}}{2}sinA+\frac{1}{2}cosA})+\sqrt{3}$
=$2\sqrt{3}sin({A+\frac{π}{6}})+\sqrt{3}$,-------(9分)
∵$0<A<\frac{2π}{3}$,
∴$\frac{π}{6}<A+\frac{π}{6}<\frac{5π}{6}$,
∴$\frac{1}{2}<sin({A+\frac{π}{6}})≤1$,
∴$2\sqrt{3}<2\sqrt{3}sin({A+\frac{π}{6}})+\sqrt{3}≤3\sqrt{3}$.
∴周长的取值范围是$({2\sqrt{3},3\sqrt{3}}]$.--------(12分)
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于基础题.

 黄冈创优卷系列答案
黄冈创优卷系列答案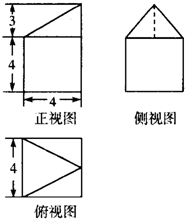
| A. | 98+6$\sqrt{5}$ | B. | 106+6$\sqrt{5}$ | C. | 114+6$\sqrt{5}$ | D. | 106+12$\sqrt{5}$ |
| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
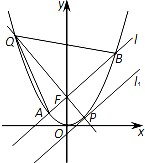 如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.
如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.