题目内容
5．已知椭圆$\frac{x^2}{100}+\frac{y^2}{36}=1$的两个焦点为F1、F2，过F2引一条斜率不为零的直线与椭圆交于点A、B，则三角形ABF1的周长是（ ）| A． | 20 | B． | 24 | C． | 32 | D． | 40 |
分析 由椭圆的定义可得：|AF1|+|AF2|=2a，|BF1|+|BF2|=2a，则三角形ABF1的周长为4a，即可得出答案．
解答 解：由椭圆方程$\frac{x^2}{100}+\frac{y^2}{36}=1$，得焦点在x轴上a2=100，则a=10，
∵点A，B在椭圆上，如右图所示，
由椭圆定义，得|AF1|+|AF2|=2a=20，|BF1|+|BF2|=2a=20，
∴△ABF1的周长=（|AF1|+|AF2|）+（|BF1|+|BF2|）=20+20=40．
故选D．
点评 本题考查焦点三角形的周长公式，考查椭圆的定义，考查数形结合思想，属于基础题．
练习册系列答案
相关题目
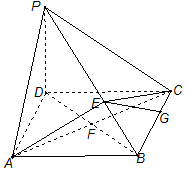如图，在四棱锥P-ABCD中，PD⊥平面ABCD，四边形ABCD是 菱形，AC=6，$BD=6\sqrt{3}$，E是PB上任意一点．
如图，D是△ABC内一点，角A，B，C的对边分别是a，b，c，且满足∠D=2∠B，cos∠D=-$\frac{1}{3}$，AD=2，△ACD的面积是4$\sqrt{2}$．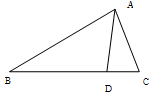
如图，在△ABC中，∠B=$\frac{π}{6}$，AB=8$\sqrt{3}$，点D在BC边上，且CD=2，cos∠ADC=$\frac{1}{7}$．