题目内容
14.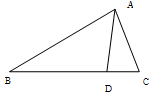 如图,在△ABC中,∠B=$\frac{π}{6}$,AB=8$\sqrt{3}$,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.
如图,在△ABC中,∠B=$\frac{π}{6}$,AB=8$\sqrt{3}$,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.(1)求sin∠BAD;
(2)求BD,AC的长.
分析 (1)由已知利用同角三角函数基本关系式可求sin∠ADC,利用两角差的正弦函数公式可求sin∠BAD的值.
(2)在△ABD中,由正弦定理得BD,在△ABC中,由余弦定理即可解得AC的值.
解答 (本题满分为12分)
解:(1)在△ADC中,因为cos∠ADC=$\frac{1}{7}$,
所以sin∠ADC=$\frac{4\sqrt{3}}{7}$.(2分)
所以sin∠BAD=sin(∠ADC-∠B)
=sin∠ADCcos B-cos∠ADCsin B(4分)
=$\frac{4\sqrt{3}}{7}$×$\frac{{\sqrt{3}}}{2}$-$\frac{1}{7}$×$\frac{1}{2}$=$\frac{11}{14}$.(6分)
(2)在△ABD中,由正弦定理得BD=$\frac{AB•sin∠BAD}{sin∠ADB}$=$\frac{{8\sqrt{3}×\frac{11}{14}}}{{\frac{{4\sqrt{3}}}{7}}}=11$.(9分)
在△ABC中,由余弦定理得:AC2=AB2+BC2-2AB•BC•cos B=${({8\sqrt{3}})^2}+{13^2}-2×8\sqrt{3}×13×\frac{{\sqrt{3}}}{2}=49$.
所以AC=7.(12分)
点评 本题主要考查了同角三角函数基本关系式,两角差的正弦函数公式,正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
5.已知椭圆$\frac{x^2}{100}+\frac{y^2}{36}=1$的两个焦点为F1、F2,过F2引一条斜率不为零的直线与椭圆交于点A、B,则三角形ABF1的周长是( )
| A. | 20 | B. | 24 | C. | 32 | D. | 40 |
9.设实数x,y满足不等式组$\left\{\begin{array}{l}x+2y-5≥0\\ 2x+y-4≤0\\ x-y+3≥0\end{array}\right.$,则x+y的最小值是( )
| A. | 3 | B. | -3 | C. | $\frac{7}{3}$ | D. | -$\frac{7}{3}$ |
19.已知$α∈(\frac{π}{2},π)$,且$sinα=\frac{4}{5}$,则tanα=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |