题目内容
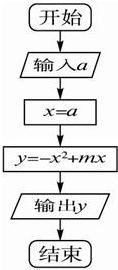 如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.
如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.(1)该程序框图解决的是一个什么问题?
(2)当输入的x值为0和4时,输出的值相等,问当输入的x值为3时,输出的值为多大?
(3)在(2)的条件下要想输出的值最大,输入的x值应为多大?
(4)在(2)条件下按照这个流程图,当x的值都大于2时,x值大的输出的y值反而小,为什么?
考点:程序框图
专题:图表型,算法和程序框图
分析:(1)模拟执行程序框图即可确定程序框图的功能是求f(x)=-x2+mx的函数值.
(2)由已知可得:f(0)=f(4),从而有-16+4m=0,即可解得m,即可求f(3)的值.
(3)由已知可得f(x)=-(x-2)2+4,从而当x=2时,f(x)max=4,即可得解.
(4)由f(x)=-(x-2)2+4,由函数图象可得:f(x)在[2,+∞)上是减函数,从而得解.
(2)由已知可得:f(0)=f(4),从而有-16+4m=0,即可解得m,即可求f(3)的值.
(3)由已知可得f(x)=-(x-2)2+4,从而当x=2时,f(x)max=4,即可得解.
(4)由f(x)=-(x-2)2+4,由函数图象可得:f(x)在[2,+∞)上是减函数,从而得解.
解答:
解:(1)该程序框图解决的是求二次函教f(x)=-x2+mx的函数值的问题;
(2)当输入的x的值为0和4时,输出的值相等,即f(0)=f(4),
因为f(0)=0,f(4)=-16+4m,
所以-16+4m=0,
所以m=4,
所以f(x)=-x2+4x,
则f(3)=-32+4×3=3,
所以当输入的x的值为3时,输出的f(x)值为3;
(3)因为f(x)=-x2+4x=-(x-2)2+4,
当x=2时,f(x)max=4,
所以要想使输出的值最大,输入的x的值应为2;
(4)因为f(x)=-(x-2)2+4,
所以函数f(x)在[2,+∞)上是减函数,
所以在[2,+∞)上,x值大的对应的函数值反而小,从而当输入的x的值大于2时,x值大的输出的f(x)值反而小.
(2)当输入的x的值为0和4时,输出的值相等,即f(0)=f(4),
因为f(0)=0,f(4)=-16+4m,
所以-16+4m=0,
所以m=4,
所以f(x)=-x2+4x,
则f(3)=-32+4×3=3,
所以当输入的x的值为3时,输出的f(x)值为3;
(3)因为f(x)=-x2+4x=-(x-2)2+4,
当x=2时,f(x)max=4,
所以要想使输出的值最大,输入的x的值应为2;
(4)因为f(x)=-(x-2)2+4,
所以函数f(x)在[2,+∞)上是减函数,
所以在[2,+∞)上,x值大的对应的函数值反而小,从而当输入的x的值大于2时,x值大的输出的f(x)值反而小.
点评:本题主要考查了二次函数的图象和性质,考查了程序框图和算法,属于基本知识的考查.

练习册系列答案
相关题目
 函数
函数