题目内容

在△ABC中，若a2+c2-b2=ac，sinAsinC=
1
4
．
（1）求角A，B；
（2）若三角形的面积为
3
，求三边a，b，c的长．
考点：余弦定理,正弦定理
专题：计算题,解三角形
分析：（1）由已知及余弦定理可得cosB=
1
2
，由0＜B＜π，可得B=
π
3
．由sinAsin（
2π
3
-A）=
1
4
，可得tan2A=
3
3
，从而解得A=
π
12
或
7π
12
．
（2）当C=
π
12
时，sin
π
12
=
6
-
2
4
，由三角形的面积为
3
，即可解得：ab=
8
3
6
-
2
=6
2
+2
6
，又sinAsinC=
1
4
，由正弦定理可得ac=R2，可得R，由a=2RsinA可求a，b=2RsinB可求b，c=2RsinC可求c．当C=
7π
12
时，同理可求a，b，c．
解答： 解：（1）∵a2+c2-b2=ac，
∴由余弦定理可得：cosB=
a2+c2-b2
2ac
=
ac
2ac
=
1
2
，
∴由0＜B＜π，可得：B=
π
3
．
∵sinAsinC=
1
4
．
∴sinAsin（
2π
3
-A）=
1
4
，可得sinA（
3
2
cosA+
1
2
sinA）=
1
4
，
∴整理可得：tan2A=
3
3
，
∵0＜A＜π，0＜2A＜2π，
∴2A=
π
6
或
7π
6
，即有：A=
π
12
或
7π
12
．
（2）由（1）可得：C=
7π
12
或
π
12
，
∴当C=
π
12
时，sin
π
12
=
6
-
2
4
，
∵三角形的面积为
3
，
∴可得：
1
2
absinC=
3
，即可解得：ab=
8
3
6
-
2
=6
2
+2
6
，
∵sinAsinC=
1
4
，由正弦定理可得：
a
2R
•
c
2R
=
1
4
，即有ac=R2，
∴R2=6
2
+2
6
，可得R=
6
2
+2
6
，
∴a=2RsinA=2
6
2
+2
6
×
6
+
2
4
=
(
6
+
2
)
6
2
+2
6
2
，
b=2RsinB=2
6
2
+2
6
×
3
2
=
18
2
+6
6
，
c=2RsinC=2
6
2
+2
6
×
6
-
2
4
=
(
6
-
2
)
6
2
+2
6
2
，
∴当C=
7π
12
时，sin
7π
12
=
6
+
2
4
，
∴a=2RsinA=2
6
2
+2
6
×
6
-
2
4
=
(
6
-
2
)
6
2
+2
6
2
，
b=2RsinB=2
6
2
+2
6
×
3
2
=
18
2
+6
6
，
c=2RsinC=2
6
2
+2
6
×
6
+
2
4
=
(
6
+
2
)
6
2
+2
6
2
．
点评：本题主要考查了正弦定理，余弦定理，三角形面积公式的应用，计算量比较大，属于基本知识的考查．
练习册系列答案
相关题目
数列{an}的前n项和为Sn，a1=2，Sn=
3
2
an-1（n∈N*）
（1）求数列{an}的通项公式；
（2）设bn=nan，求数列{bn}的前n项和Tn．
函数f（x）=
x2-2x-3
的递增区间为（　　）
A、[3，+∞）
B、[1，+∞）
C、（-∞，-1]
D、（-∞，1]
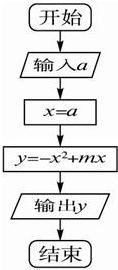如图所示的程序框图，根据该图和下列各个小题的条件回答下面的几个小题．
（1）该程序框图解决的是一个什么问题？
（2）当输入的x值为0和4时，输出的值相等，问当输入的x值为3时，输出的值为多大？
（3）在（2）的条件下要想输出的值最大，输入的x值应为多大？
（4）在（2）条件下按照这个流程图，当x的值都大于2时，x值大的输出的y值反而小，为什么？
下列结论：①?a，b∈（0，+∞）当a+b=1时
1
a
+
1
b
=3；②f（x）=lg（x2+ax+1），定义域为R，则-2＜a＜2；③x+y≠3是x≠1或y≠2成立的充分不必要条件；④f（x）=
1-x
+
x+3
最大值与最小值的比为
2
．
其中正确结论的序号为
 
．
比较2n•n!与（n+1）n（n∈N*）的大小关系，并给出证明．
下面的四个不等式：①a2+b2+c2≥ab+bc+ca；②a（1-a）≤
1
4
；③
a
b
+
b
a
≥2；④（a2+b2）•（c2+d2）≥（ac+bd）2．其中一定成立的序号依次是
 
．
圆x2+y2=25截直线4x-3y=20所得弦的中垂线方程是（　　）
A、y=
3
4
x
B、y=-
3
4
x
C、y=
4
3
x
D、y=-
4
3
x
已知f（x）二阶可导，y=f（cosx），求y″．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网