题目内容
根据数列0,1,3,4,5,6,8,9,10…的项构造出一个新的数列,并写出它的一个通项公式.
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:由数列0,1,3,4,5,6,8,9,10…,从第二项开始:每一项减去它的前一项的差可得周期数列{an}:1,2,1,1,1,2,1,1,….即可得出通项公式.
解答:
解:由数列0,1,3,4,5,6,8,9,10…,
从第二项开始:每一项减去它的前一项的差可得数列{an}:1,2,1,1,1,2,1,1,….
可得周期性
∴数列an=
,k∈N*.
从第二项开始:每一项减去它的前一项的差可得数列{an}:1,2,1,1,1,2,1,1,….
可得周期性
∴数列an=
|
点评:本题考查了构造法、数列的周期性、通项公式,考查了推理能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
的递增区间为( )
| x2-2x-3 |
| A、[3,+∞) |
| B、[1,+∞) |
| C、(-∞,-1] |
| D、(-∞,1] |
已知F1,F2是双曲线
-
=1(a>0,b>0)的左右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(2,+∞) | ||||
B、(
| ||||
C、(
| ||||
D、(1,
|

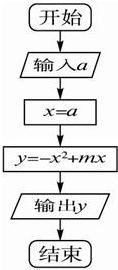 如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.
如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.