题目内容
已知奇函数y=f(x)满足当x≥0时,f(x)=2x+x-a,则f(-1)= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先根据f(0)=0求出a的值,然后根据奇函数的性质,将f(-1)转化为f(1)的函数值.
解答:
解:因为f(x)是奇函数,且在x=0时有定义,所以f(0)=1-a=0,所以a=1.
所以x≥0时,f(x)=2x+x-1,所以f(1)=2.
所以f(-1)=-f(1)=-2.
故答案为-2.
所以x≥0时,f(x)=2x+x-1,所以f(1)=2.
所以f(-1)=-f(1)=-2.
故答案为-2.
点评:本题综合考查了函数的奇函数的性质,体现转化思想在解题中的作用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
函数f(x)=
的递增区间为( )
| x2-2x-3 |
| A、[3,+∞) |
| B、[1,+∞) |
| C、(-∞,-1] |
| D、(-∞,1] |
圆x2+y2=25截直线4x-3y=20所得弦的中垂线方程是( )
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
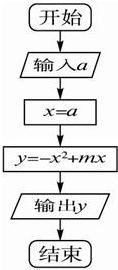 如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.
如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.