题目内容
设f(x)=sin(2x+
),则下列结论正确的是: .
①f(x)的最小正周期为π;
②f(x)的图象关于直线x=
对称;
③f(x)的图象关于点(
,0)对称;
④把f(x)图象左移
个单位,得到一个偶函数的图象;
⑤f(x)在[0,
]上为单调递增函数.
| π |
| 3 |
①f(x)的最小正周期为π;
②f(x)的图象关于直线x=
| π |
| 3 |
③f(x)的图象关于点(
| π |
| 4 |
④把f(x)图象左移
| π |
| 12 |
⑤f(x)在[0,
| π |
| 6 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据函数y=Asin(ωx+φ)的图象性质,逐一判断各个选项是否正确,从而得出结论.
解答:
解:对于函数f(x)=sin(2x+
),它的最小正周期为
=π,故①正确;
当x=
时,f(x)=sinπ=0,不是最值,故f(x)的图象不关于直线x=
对称,故②错误;
当x=
时,f(x)=sin(
+
)=
≠0,故f(x)的图象不关于点(
,0)对称,故③错误;
把f(x)图象左移
个单位,得到y=sin[2(x+
)+
]=cos2x的图象,
故所得函数为偶函数,故④正确;
在[0,
]上,2x+
∈[
,
],f(x)不是单调递增函数,故⑤错误,
故答案为:①④.
| π |
| 3 |
| 2π |
| 2 |
当x=
| π |
| 3 |
| π |
| 3 |
当x=
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
把f(x)图象左移
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
故所得函数为偶函数,故④正确;
在[0,
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
故答案为:①④.
点评:本题主要考查函数y=Asin(ωx+φ)的图象性质,属于中档题.

练习册系列答案
相关题目
圆x2+y2=25截直线4x-3y=20所得弦的中垂线方程是( )
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
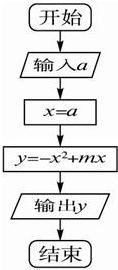 如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.
如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.