题目内容
定义在[1,+∞)上的函数f(x)满足:①当2≤x≤4时,f(x)=1-|x-3|;②f(2x)=cf(x)(c为正常数),
若函数的所有极大值点都落在同一直线上,则常数c的值是( )
若函数的所有极大值点都落在同一直线上,则常数c的值是( )
| A、1 | ||
| B、±2 | ||
C、
| ||
| D、1或2 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:由已知中定义在[1,+∞)上的函数f(x)满足:①f(2x)=cf(x)(c为正常数);②当2≤x≤4时,f(x)=1-|x-3|.我们可得分段函数f(x)的解析式,进而求出三个函数的极值点坐标,进而根据三点共线,则任取两点确定的直线斜率相等,可以构造关于c的方程,解方程可得答案.
解答:
解:∵当2≤x≤4时,f(x)=1-|x-3|.
当1≤x<2时,2≤2x<4,
则f(x)=
f(2x)=
(1-|2x-3|),
此时当x=
时,函数取极大值
;
当2≤x≤4时,
f(x)=1-|x-3|;
此时当x=3时,函数取极大值1;
当4<x≤8时,2<
≤4,
则f(x)=cf(
)=c(1-|
-3|),
此时当x=6时,函数取极大值c.
∵函数的所有极大值点均落在同一条直线上,
即点(
,
),(3,1),(6,c)共线,
∴
=
,
解得c=1或2.
故选D.
当1≤x<2时,2≤2x<4,
则f(x)=
| 1 |
| c |
| 1 |
| c |
此时当x=
| 3 |
| 2 |
| 1 |
| c |
当2≤x≤4时,
f(x)=1-|x-3|;
此时当x=3时,函数取极大值1;
当4<x≤8时,2<
| x |
| 2 |
则f(x)=cf(
| x |
| 2 |
| x |
| 2 |
此时当x=6时,函数取极大值c.
∵函数的所有极大值点均落在同一条直线上,
即点(
| 3 |
| 2 |
| 1 |
| c |
∴
1-
| ||
|
| c-1 |
| 3 |
解得c=1或2.
故选D.
点评:本题考查的知识点是三点共线,函数的极值,其中根据已知分析出分段函数f(x)的解析式,进而求出三个函数的极值点坐标,是解答本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
圆心在C(-3,4),且半径为
的圆的方程为( )
| 5 |
| A、(x-3)2+(y+4)2=5 | ||
B、(x+3)2+(y-4)2=
| ||
| C、(x+3)2+(y-4)2=5 | ||
D、(x-3)2+(y+4)2=
|
若关于x的不等式x2+ax-2>0在区间[1,5]上有解,则实数a的取值范围为( )
A、(-
| ||
B、[-
| ||
| C、(1,+∞) | ||
| D、(-∞,-1) |
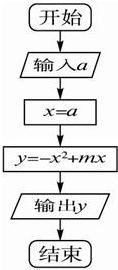 如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.
如图所示的程序框图,根据该图和下列各个小题的条件回答下面的几个小题.