题目内容
13. 如图所示的程序框图中,若f(x)=x2,g(x)=x,且h(x)≥m恒成立,则m的最大值是( )
如图所示的程序框图中,若f(x)=x2,g(x)=x,且h(x)≥m恒成立,则m的最大值是( )| A. | 4 | B. | 3 | C. | 1 | D. | 0 |
分析 由已知中的程序框图可得该程序的功能是计算并输出分段函数:h(x)=$\left\{\begin{array}{l}{{x}^{2},x≥1或x≤0}\\{x,0<x<1}\end{array}\right.$的值,数形结合求出h(x)的最小值,可得答案.
解答 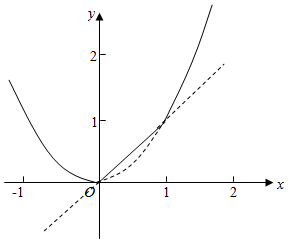 解:由已知中的程序框图可得该程序的功能是:
解:由已知中的程序框图可得该程序的功能是:
计算并输出分段函数:h(x)=$\left\{\begin{array}{l}{{x}^{2},x≥1或x≤0}\\{x,0<x<1}\end{array}\right.$的值,
在同一坐标系,画出f(x)=x2,g(x)=x的图象如下图所示:(实线部分为h(x)的图象)
由图可知:当x=0时,h(x)取最小值0,
又∵h(x)≥m恒成立,
∴m≤0,即m的最大值是0;
故选:D
点评 本题主要考查了程序框图,分段函数的应用,函数恒成立问题;考查了数形结合的解答方法;属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15.函数f(x)=x2+3x-4 的单调递增区间是( )
| A. | (-∞,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,+∞) | C. | [$\frac{3}{2}$,4) | D. | (-1,$\frac{3}{2}$] |
1.设等差数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n成等差数列,类比以上结论,设等比数列{bn}的前
n项积为Tn,则( )
n项积为Tn,则( )
| A. | Tn,T2n,T3n成等比数列 | B. | Tn,T2n-Tn,T3n-T2n成等差数列 | ||
| C. | Tn,$\frac{{T}_{2n}}{{T}_{n}}$,$\frac{{T}_{3n}}{{T}_{2n}}$成等比数列 | D. | Tn,T2n-Tn,T3n-T2n成等比数列 |
18.在平面直角坐标系中,O为坐标原点,A为单位圆上一点,以x轴为始边,OA为终边的角为θ(θ≠kπ+$\frac{π}{2}$,k∈Z),若将OA绕O点顺时针旋转$\frac{3π}{2}$至OB,则点B的坐标为( )
| A. | (-cosθ,sinθ) | B. | (cosθ,-sinθ) | C. | (-sinθ,cosθ) | D. | (sinθ,-cosθ) |
5.在(x-$\frac{2}{\sqrt{x}}$)6展开式中,常数项为( )
| A. | -192 | B. | -160 | C. | 60 | D. | 240 |