题目内容
15.函数f(x)=x2+3x-4 的单调递增区间是( )| A. | (-∞,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,+∞) | C. | [$\frac{3}{2}$,4) | D. | (-1,$\frac{3}{2}$] |
分析 判断二次函数的开口方向,求出对称轴,即可得到结果.
解答 解:函数f(x)=x2+3x-4 的开口向上,对称轴为:x=$-\frac{3}{2}$,
函数f(x)=x2+3x-4 的单调递增区间是:[-$\frac{3}{2}$,+∞).
故选:B.
点评 本题考查二次函数的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
10.sin$\frac{5π}{3}$等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
7.已知cos(α-$\frac{π}{6}$)=-$\frac{1}{3}$,且α∈(0,π),则sinα等于( )
| A. | $\frac{{2\sqrt{6}-1}}{6}$ | B. | $\frac{{2\sqrt{2}+\sqrt{3}}}{6}$ | C. | $\frac{{2\sqrt{6}+1}}{6}$ | D. | $\frac{{2\sqrt{2}-\sqrt{3}}}{6}$ |
4. 如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )
如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )
 如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )
如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )| A. | $\overrightarrow{AB}•\overrightarrow{AC}=0$ | B. | $\overrightarrow{AD}•\overrightarrow{BC}=0$ | C. | $\overrightarrow{AB}•\overrightarrow{AD}=0$ | D. | $\overrightarrow{AD}•\overrightarrow{AC}=0$ |
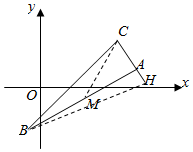 如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为
如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为 如图所示的程序框图中,若f(x)=x2,g(x)=x,且h(x)≥m恒成立,则m的最大值是( )
如图所示的程序框图中,若f(x)=x2,g(x)=x,且h(x)≥m恒成立,则m的最大值是( )