题目内容
1.设等差数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n成等差数列,类比以上结论,设等比数列{bn}的前n项积为Tn,则( )
| A. | Tn,T2n,T3n成等比数列 | B. | Tn,T2n-Tn,T3n-T2n成等差数列 | ||
| C. | Tn,$\frac{{T}_{2n}}{{T}_{n}}$,$\frac{{T}_{3n}}{{T}_{2n}}$成等比数列 | D. | Tn,T2n-Tn,T3n-T2n成等比数列 |
分析 利用等差数列与等比数列的定义,写出类比的结论.
解答 解:由于等差数列的定义是后一项减去前一项而等比数列的定义是后一项除以前一项,
在运算上升了一级,
故将差类比成比,
故Tn,$\frac{{T}_{2n}}{{T}_{n}}$,$\frac{{T}_{3n}}{{T}_{2n}}$成等比数列,
故选:C.
点评 本题考查通过类比推理将差类比成比,属于基础题.

练习册系列答案
相关题目
4. 如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )
如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )
 如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )
如图,D为等腰三角形ABC底边BC的中点,则下列等式恒成立的是( )| A. | $\overrightarrow{AB}•\overrightarrow{AC}=0$ | B. | $\overrightarrow{AD}•\overrightarrow{BC}=0$ | C. | $\overrightarrow{AB}•\overrightarrow{AD}=0$ | D. | $\overrightarrow{AD}•\overrightarrow{AC}=0$ |
16.已知a=30.7,b=0.72016,c=log2017$\frac{1}{2016}$,则( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
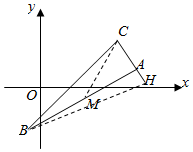 如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为
如图,已知△ABC的顶点A(5,1),AC边上的高BH所在直线为 如图所示的程序框图中,若f(x)=x2,g(x)=x,且h(x)≥m恒成立,则m的最大值是( )
如图所示的程序框图中,若f(x)=x2,g(x)=x,且h(x)≥m恒成立,则m的最大值是( )