题目内容
设a∈R,e为自然对数的底数,函数f(x)=
(Ⅰ)当a=0时,求f(x)在x=e处的切线方程;
(Ⅱ)当a<-1时,是否存在a使f(x)在[a,-a]上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
|
(Ⅰ)当a=0时,求f(x)在x=e处的切线方程;
(Ⅱ)当a<-1时,是否存在a使f(x)在[a,-a]上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)把a=0代入第二段函数,求导后得到函数在x=e处的导数,再求出f(e),然后由直线方程的点斜式得切线方程;
(Ⅱ)分别对两段函数在[a,1]上和[1,-a]上求导,由导函数小于0得a的范围,再由x=1时上段函数的函数值大于等于下段函数的函数值求得a的范围,最后去交集得答案.
(Ⅱ)分别对两段函数在[a,1]上和[1,-a]上求导,由导函数小于0得a的范围,再由x=1时上段函数的函数值大于等于下段函数的函数值求得a的范围,最后去交集得答案.
解答:
解:(Ⅰ)当a=0时,f(x)=(-lnx+x)•e,x>1.
∴f′(x)=(1-
)•e,
则f′(e)=e-1.
又f(e)=e2-e.
∴y-e2+e=(e-1)(x-e),
整理得:(e-1)x-y=0;
(Ⅱ)当a<-1时,-a>1,则区间[a,-a]的左端点小于-1,右端点大于1,
要使f(x)在[a,-a]上为减函数,
即f(x)=(-2x3+3ax2+6ax-4a2-6a)•ex ①在[a,1]上为减函数,
f(x)=[(6a-1)lnx+x+
+15a]•e ②在[1,-a]上为减函数,
且(-2+3a+6a-4a2-6a)•e≥(1+a+15a)•e ③.
解③得:-3≤a≤-
.
对①求导得:f′(x)=[-2x3+(3a-6)x2+12ax-4a2]•ex,
要使f′(x)≤0在[a,1]上成立,
则g(x)=-2x3+(3a-6)x2+12ax-4a2≤0在[a,1]上成立,
由g′(x)=-6x2+(6a-12)x+12a=0,得x=a或x=-2.
当a≥-2时,g(x)在[a,1]上为减函数,
由g(a)=-2a3+3a3-6a2+12a2-4a2=a3+2a2≤0,
得a≤-2,
∴a=-2.
当a<-2时,g(x)在[a,1]上的最大值为g(-2)=16+12a-24-24a-4a2=-4a2-12a-8.
由g(-2)≤0,解得:a≤-2或a≥-1.
∴a<-2.
对②求导得:f′(x)=(
+1-
)•e=
•e.
要使f′(x)≤0在[1,-a]上成立,
则h(x)=x2+(6a-1)x-a≤0在[1,-a]上成立,
即
,解得:a≤0.
综上,存在实数a∈[-3,-2],使f(x)在[a,-a]上为减函数.
∴f′(x)=(1-
| 1 |
| x |
则f′(e)=e-1.
又f(e)=e2-e.
∴y-e2+e=(e-1)(x-e),
整理得:(e-1)x-y=0;
(Ⅱ)当a<-1时,-a>1,则区间[a,-a]的左端点小于-1,右端点大于1,
要使f(x)在[a,-a]上为减函数,
即f(x)=(-2x3+3ax2+6ax-4a2-6a)•ex ①在[a,1]上为减函数,
f(x)=[(6a-1)lnx+x+
| a |
| x |
且(-2+3a+6a-4a2-6a)•e≥(1+a+15a)•e ③.
解③得:-3≤a≤-
| 1 |
| 4 |
对①求导得:f′(x)=[-2x3+(3a-6)x2+12ax-4a2]•ex,
要使f′(x)≤0在[a,1]上成立,
则g(x)=-2x3+(3a-6)x2+12ax-4a2≤0在[a,1]上成立,
由g′(x)=-6x2+(6a-12)x+12a=0,得x=a或x=-2.
当a≥-2时,g(x)在[a,1]上为减函数,
由g(a)=-2a3+3a3-6a2+12a2-4a2=a3+2a2≤0,
得a≤-2,
∴a=-2.
当a<-2时,g(x)在[a,1]上的最大值为g(-2)=16+12a-24-24a-4a2=-4a2-12a-8.
由g(-2)≤0,解得:a≤-2或a≥-1.
∴a<-2.
对②求导得:f′(x)=(
| 6a-1 |
| x |
| a |
| x2 |
| x2+(6a-1)x-a |
| x2 |
要使f′(x)≤0在[1,-a]上成立,
则h(x)=x2+(6a-1)x-a≤0在[1,-a]上成立,
即
|
综上,存在实数a∈[-3,-2],使f(x)在[a,-a]上为减函数.
点评:本题考查利用导数研究曲线上某点处的切线方程,考查了分段函数的单调性的判断,考查了学生的计算能力,是压轴题.

练习册系列答案
相关题目
已知集合A={1,2},B={a,a2,2},若A∩B={1,2},则a的值为( )
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、-
|
实数x,y满足条件
,则22x-y的最小值为( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、4 |
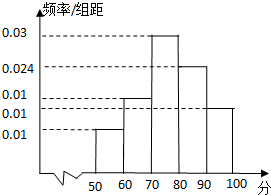 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.