题目内容
已知A(2,0),B(0,2),C(cos θ,sin θ),O为坐标原点
(1) 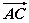 ·
·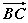 =-
=-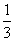 ,求sin 2θ的值.
,求sin 2θ的值.
(2)若|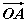 +
+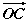 |=
|=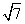 ,且θ∈(-π,0),求
,且θ∈(-π,0),求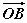 与
与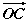 的夹角.
的夹角.
解析:(1) 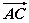 =(cos θ,sin θ)-(2,0)
=(cos θ,sin θ)-(2,0)
=(cos θ-2,sin θ)
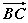 =(cos θ,sin θ)-(0,2)=(cos θ,sin θ-2).
=(cos θ,sin θ)-(0,2)=(cos θ,sin θ-2).
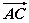 ·
·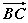 =cos θ(cos θ-2)+sin θ(sin θ-2)
=cos θ(cos θ-2)+sin θ(sin θ-2)
=cos2θ-2cos θ+sin2θ-2sin θ
=1-2(sin θ+cos θ)=-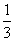 .
.
∴sin θ+cos θ= ,
,
∴1+2sin θcos θ= ,
,
∴sin 2θ= -1=-
-1=- .
.
(2)∵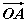 =(2,0),
=(2,0),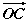 =(cos θ,sin θ),
=(cos θ,sin θ),
∴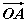 +
+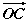 =(2+cos θ,sin θ),
=(2+cos θ,sin θ),
∴|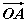 +
+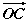 |=
|= =
=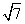 .
.
即4+4cos θ+cos2θ+sin2θ=7.
∴4cos θ=2,即cos θ= .
.
∵-π<θ<0,∴θ=-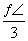 .
.
又∵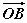 =(0,2),
=(0,2),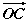 =
= ,
,
∴cos 〈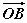 ,
,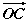 〉=
〉= =
= =-
=- .
.
∴〈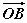 ,
,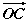 〉=
〉= .
.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 B.8-4
B.8-4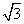 C.1 D.
C.1 D.
 =m
=m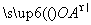 +n
+n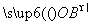 ,(m,n∈R).
,(m,n∈R). 点E为BC的中点,点F在边CD上,若
点E为BC的中点,点F在边CD上,若 ,则
,则 的值是( ).
的值是( ).
 B.2 C.
B.2 C. D.3
D.3 且
且 = .
= .
 ,则向量a与c的夹角为( )
,则向量a与c的夹角为( ) C.
C.  D.
D. 
 ,
,  ,若
,若 ,则
,则 的值为 .
的值为 .  2,n
2,n N+), 则bn=
N+), 则bn=