题目内容
已知O,A,B三点不共线,且 =m
=m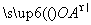 +n
+n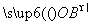 ,(m,n∈R).
,(m,n∈R).
(1)若m+n=1,求证:A,P,B三点共线;
(2)若A,P,B三点共线,求证:m+n=1.
证明 (1)m,n∈R,且m+n=1,
∴ =m
=m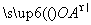 +n
+n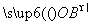 =m
=m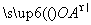 +(1-m)
+(1-m)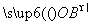 ,
,
即 -
-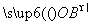 =m(
=m(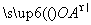 -
-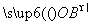 ).
).
∴ =m
=m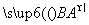 ,而
,而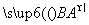 ≠0,且m∈R.
≠0,且m∈R.
故 与
与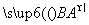 共线,又
共线,又 ,
,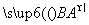 有公共点B.
有公共点B.
∴A,P,B三点共线.
(2)若A,P,B三点共线,则 与
与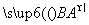 共线,故存在实数λ,使
共线,故存在实数λ,使 =λ
=λ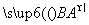 ,∴
,∴ -
-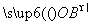 =λ(
=λ(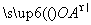 -
-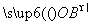 ).
).
即 =λ
=λ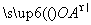 +(1-λ)
+(1-λ)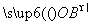 .
.
由 =m
=m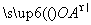 +n
+n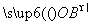 .
.
故m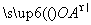 +n
+n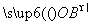 =λ
=λ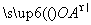 +(1-λ)
+(1-λ)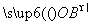 .
.
又O,A,B不共线,∴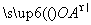 ,
,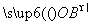 不共线.
不共线.
由平面向量基本定理得
∴m+n=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若x∈
(ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若x∈ ,则f(x)的取值范围是________.
,则f(x)的取值范围是________.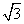 km,那么x的值为( ).
km,那么x的值为( ).  =
=
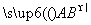 +
+
 ,则△ABM与△ABC的面积之比为________.
,则△ABM与△ABC的面积之比为________. =(1,2),
=(1,2), =(3,4),则
=(3,4),则 =( )
=( )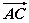 ·
·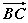 =-
=-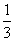 ,求sin 2θ的值.
,求sin 2θ的值.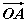 +
+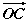 |=
|=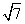 ,且θ∈(-π,0),求
,且θ∈(-π,0),求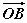 与
与 中,
中, ,则
,则 =( )
=( )