题目内容
10.给出下列实际问题:①一种药物对某种病的治愈率;
②两种药物治疗同一种病是否有关系;
③吸烟者得肺病的概率;
④吸烟人群是否与性别有关系;
⑤上网与青少年的犯罪率是否有关系.
其中,用独立性检验可以解决的问题有②④⑤.
分析 利用独立性检验的定义,即可得出结论.
解答 解:独立性检验主要对两个分类变量是否有关系进行检验,主要涉及两种变量对同一种事情的影响,或者是两种变量在同一问题上体现的区别等,由此可得用独立性检验可以解决的问题有②④⑤,
故答案为②④⑤.
点评 独立性检验主要对两个分类变量是否有关系进行检验,主要涉及两种变量对同一种事情的影响,或者是两种变量在同一问题上体现的区别等.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
18.已知复数z满足$iz=\frac{4+3i}{1+2i}$,则复数z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.要得到函数$y=3sin(x+\frac{π}{2})$的图象,只需将函数y=3sin(2x-$\frac{π}{6}$)的图象上所有点的( )
| A. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. |
19.已知函数f(x)=x2+2x+m(m∈R)的最小值为-1,则${∫}_{1}^{2}$f(x)dx=( )
| A. | 2 | B. | $\frac{16}{3}$ | C. | 6 | D. | 7 |
20.若向量$\overrightarrow{a}$(-1,1),$\overrightarrow{b}$(3,-2),则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{6}$ | B. | 5 | C. | $\sqrt{5}$ | D. | 6 |
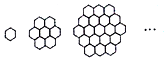 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.