题目内容
15.已知△ABC中,tanA,tanB是方程x2+ax+4=0的两个实数根:(1)若a=-8,求tanC的值;
(2)求tanC的最小值,并指出此时对应的tanA,tanB的值.
分析 (1)由根与系数的关系写出tanA+tanB=8,tanAtanB=4;利用三角形内角和定理与两角和的正切公式计算即可;
(2)由△≥0以及根与系数的关系,求出a≤-4;再利用三角形内角和定理与两角和的正切公式,求出tanC的最小值以及此时对应的tanA、tanB的值.
解答 解:(1)a=8时,x2-8x+4=0,
∴tanA+tanB=8,tanAtanB=4;
∴tanC=tan[π-(A+B)]
=-tan(A+B)
=$\frac{tanA+tanB}{tanAtanB-1}$
=$\frac{8}{3}$:
(2)由题意,△=a2-16≥0,
解得a≥4或a≤-4;
又tanAtanB=4>0,
∴$\left\{\begin{array}{l}{tanA>0}\\{tanB>0}\end{array}\right.$,
∴tanA+tanB=-a>0,
∴a<0,
即a≤-4;
∴tanC=-tan(A+B)=$\frac{tanA+tanB}{tanAtanB-1}$=$\frac{-a}{3}$≥$\frac{4}{3}$,
∴tanC的最小值是$\frac{4}{3}$,此时对应的tanA=tanB=2.
点评 本题考查了根与系数的关系以及三角形内角和定理与两角和的正切公式应用问题,是基础题.

练习册系列答案
相关题目
5.一个几何体的三视图,则它的体积为( )
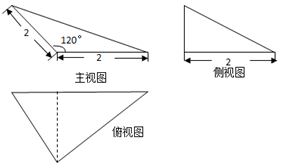

| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
3.两个变量y和x进行回归分析,得到一组样本数据(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )
| A. | 由样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小说明拟合效果越好 | |
| D. | 若变量y和x之间的相关系数为r=-0.9462,则变量y和x之间具有线性相关关系 |
20.$y=sin({ωx+\frac{5π}{6}})({0<ω<π})$的图象与坐标轴的所有交点中,距离原点最近的两个点为$({0,\frac{1}{2}})$和$({\frac{1}{2},0})$,那么该函数图象的所有对称轴中,距离y轴最近的一条对称轴是( )
| A. | x=-1 | B. | $x=-\frac{1}{2}$ | C. | x=1 | D. | $x=\frac{3}{2}$ |
7. 某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:
某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:
单位:亿元
(1)画出散点图,判断x与y是否具有相关关系;
(2)已知$\widehatb=0.842,\widehata=-0.943$,请写出y对x的回归直线方程,并计算出1999年的随机误差效应;
(3)估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
 某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:
某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:单位:亿元
| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 货币收入x | 40 | 42 | 44 | 47 | 50 |
| 购买商品支出y | 33 | 34 | 36 | 39 | 41 |
(2)已知$\widehatb=0.842,\widehata=-0.943$,请写出y对x的回归直线方程,并计算出1999年的随机误差效应;
(3)估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
4.在△ABC中,已知A=30°,a=8,则△ABC的外接圆直径是( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
5.一个四棱锥的三视图在1×1的方格中显示如图,则此几何体的体积为( )


| A. | 8 | B. | 4 | C. | 3 | D. | $\frac{8}{3}$ |