题目内容
6.如图所示,在矩形ABCD中,E是CD上的点,以AE为折痕将△ADE向上折起,连接BD,BE,求证:(1)若AD⊥BD,则平面ABD⊥平面BDE;
(2)以上命题的逆命题是否成立?若成立,给出证明,否则,举出反例.
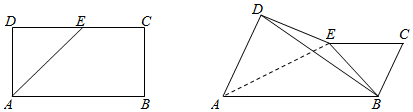
分析 (1)由已知推导出AD⊥DE,AD⊥BD,由此能证明平面ABD⊥平面BDE.
(2)推导出AD⊥DE,由平面ABD⊥平面BDE,得AD⊥平面BDE,由此能证明AD⊥BD.
解答 证明:(1)∵在矩形ABCD中,E是CD上的点,以AE为折痕将△ADE向上折起,连接BD,BE,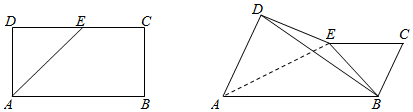
∴AD⊥DE,
∵AD⊥BD,BD∩DE=D,
∴平面ABD⊥平面BDE.
解:(2)以上命题的逆命题成立.
证明如下:
∵在矩形ABCD中,E是CD上的点,以AE为折痕将△ADE向上折起,连接BD,BE,
∴AD⊥DE,
∵平面ABD⊥平面BDE,
∴AD⊥平面BDE,
∵BD?平面BDE,∴AD⊥BD.
点评 本题考查面面垂直的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
16.在△ABC中,角A,B,C对应的边分别为a,b,c,若b-acosB=acosC-c,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
14.已知p:“a≥$\frac{12}{t+\frac{1}{t}}$对t∈(0,+∞)恒成立”,q:“直线x-2y+a=0与曲线y-1=$\sqrt{4+2x-{x}^{2}}$有2个公共点”,则¬p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为30°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
| A. | ($\frac{1}{2}$,$\frac{2\sqrt{3}}{3}$) | B. | [$\frac{1}{2}$,$\frac{2\sqrt{3}}{3}$] | C. | ($\frac{\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |
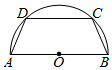 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.