题目内容
6.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的离心率是$\frac{\sqrt{13}}{2}$.分析 求得双曲线的a,b,c,运用离心率公式e=$\frac{c}{a}$,计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的a=2,b=3,
可得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{13}$,
即有离心率e=$\frac{c}{a}$=$\frac{\sqrt{13}}{2}$.
故答案为:$\frac{\sqrt{13}}{2}$.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的基本量的关系,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知p:“a≥$\frac{12}{t+\frac{1}{t}}$对t∈(0,+∞)恒成立”,q:“直线x-2y+a=0与曲线y-1=$\sqrt{4+2x-{x}^{2}}$有2个公共点”,则¬p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为30°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
| A. | ($\frac{1}{2}$,$\frac{2\sqrt{3}}{3}$) | B. | [$\frac{1}{2}$,$\frac{2\sqrt{3}}{3}$] | C. | ($\frac{\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |
1.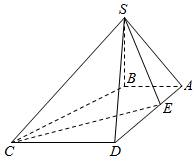 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.若双曲线$\frac{{x}^{2}}{3}$-$\frac{16{y}^{2}}{{p}^{2}}$=1的一个焦点在抛物线y2=2px的准线上,则该双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | 2 |
16.sin1°,sin1,sinπ°的大小顺序是( )
| A. | sin1°<sin1<sinπ° | B. | sin1°<sinπ°<sin1 | ||
| C. | sinπ°<sin1°<sin1 | D. | sin1<sin1°<sinπ° |
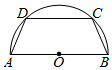 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.