题目内容
四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，AA′⊥平面ABCD．（1）求证：A′C∥平面BDE；
（2）求证：平面A′AC⊥平面BDE；
（3）求三棱锥A-BDE的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题：综合题,空间位置关系与距离
分析：（1）设BD交AC于M，连结ME，证明ME∥A′C，即可证明A′C∥平面BDE；
（2）证明BD⊥平面A′AC，即可证明平面A′AC⊥平面BDE；
（3）利用等体积转换，即可求三棱锥A-BDE的体积．
（2）证明BD⊥平面A′AC，即可证明平面A′AC⊥平面BDE；
（3）利用等体积转换，即可求三棱锥A-BDE的体积．
解答：
（1）证明：设BD交AC于M，连结ME．
∵ABCD为正方形，所以M为AC中点，
又∵E为A′A的中点，
∴ME为△A′AC的中位线
∴ME∥A′C
又∵ME?平面BDE，A′C?平面BDE
∴A′C∥平面BDE．…..（4分）
（2）证明：∵ABCD为正方形，∴BD⊥AC
∵A′A⊥平面ABCE，BD⊥平面ABCD，
∴A′A⊥BD．
又AC∩A′A=A，
∵AC?面A′AC，AA′?面A′AC，∴BD⊥平面A′AC
∵BD?平面BDE
∴平面A′AC⊥平面BDE．…．（8分）
（3）解：V=VA-BDE=VE-ABD=
…（12分）
（1）证明：设BD交AC于M，连结ME．∵ABCD为正方形，所以M为AC中点，
又∵E为A′A的中点，
∴ME为△A′AC的中位线
∴ME∥A′C
又∵ME?平面BDE，A′C?平面BDE
∴A′C∥平面BDE．…..（4分）
（2）证明：∵ABCD为正方形，∴BD⊥AC
∵A′A⊥平面ABCE，BD⊥平面ABCD，
∴A′A⊥BD．
又AC∩A′A=A，
∵AC?面A′AC，AA′?面A′AC，∴BD⊥平面A′AC
∵BD?平面BDE
∴平面A′AC⊥平面BDE．…．（8分）
（3）解：V=VA-BDE=VE-ABD=
| a3 |
| 12 |
点评：本题考查线面平行、垂直的判定，考查面面垂直，考查锥体体积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图，在底面是矩形的四棱锥P-ABCD中，PA⊥底面ABCD，E，F分别是PC，PD的中点，PA=AB=1，BC=2．
所有棱长均为1的四棱柱ABCD-A1B1C1C1如图所示，∠DAB=60°，CC1⊥A1C1．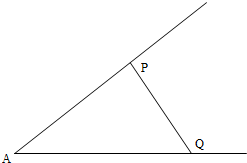
如图，已知锐角∠A为定角，点P，Q分别在∠A的两边上，且△APQ的面积为定值S，当P，Q在什么位置时，PQ长最短．
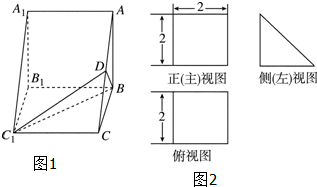直三棱柱ABC-A1B1C1的直观图（图1）及三视图（图2）如图所示，D为AC的中点