题目内容
 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E,F分别是PC,PD的中点,PA=AB=1,BC=2.(1)求证:EF∥平面PAB;
(2)求证:平面PAD⊥平面PDC.
(3)求四棱锥P-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)由E、F分别是PC、PD的中点,可由三角形中位线定理得到EF∥CD,进而根据底面是矩形,对边平行得到EF∥AB,结合线面平行的判定定理得到EF∥平面PAB;
(2)由PA⊥底面ABCD,底面ABCD是矩形,可得PA⊥CD及AD⊥CD,进而由线面垂直的判定定理得到DC⊥平面PAD,进而由面面垂直的判定定理得到平面PAD⊥平面PDC;
(3)利用VP-ABCD=
SABCD•PA,即可求出四棱锥P-ABCD的体积.
(2)由PA⊥底面ABCD,底面ABCD是矩形,可得PA⊥CD及AD⊥CD,进而由线面垂直的判定定理得到DC⊥平面PAD,进而由面面垂直的判定定理得到平面PAD⊥平面PDC;
(3)利用VP-ABCD=
| 1 |
| 3 |
解答:
(1)证明: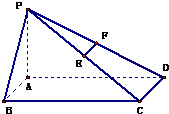 ∵E、F分别是PC、PD的中点,
∵E、F分别是PC、PD的中点,
∴EF∥CD. (2分)
∵底面ABCD是矩形,
∴CD∥AB.
∴EF∥AB. (4分)
又AB?平面PAB,EF?平面PAB,
∴EF∥平面PAB. (7分)
(2)解:∵PA⊥底面ABCD,CD?底面ABCD
∴PA⊥CD. (8分)
∵底面ABCD是矩形,AD⊥CD.
又PA∩AD=A,AP?面PAD,AD?面PAD,
∴DC⊥平面PAD.
∵DC?平面PDC,
∴平面PAD⊥平面PDC. (10分)
(3)解:∵在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2,
∴VP-ABCD=
SABCD•PA=
×1×2×1=
…(12分)
 ∵E、F分别是PC、PD的中点,
∵E、F分别是PC、PD的中点,∴EF∥CD. (2分)
∵底面ABCD是矩形,
∴CD∥AB.
∴EF∥AB. (4分)
又AB?平面PAB,EF?平面PAB,
∴EF∥平面PAB. (7分)
(2)解:∵PA⊥底面ABCD,CD?底面ABCD
∴PA⊥CD. (8分)
∵底面ABCD是矩形,AD⊥CD.
又PA∩AD=A,AP?面PAD,AD?面PAD,
∴DC⊥平面PAD.
∵DC?平面PDC,
∴平面PAD⊥平面PDC. (10分)
(3)解:∵在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2,
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,考查四棱锥的体积.其中(1)的关键是证得EF∥AB,(2)的关键是证得DC⊥平面PAD.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知x,y∈R,i为虚数单位,且xi-y=-1+i,则(1-i)x+y的值是( )
| A、2 | B、-2i | C、-4 | D、2i |
如图,圆内的两条弦AB,CD相交于圆内一点P,已知PA=PB=6,PC=
PD,则CD=( )
| 1 |
| 4 |

| A、15 | B、18 | C、12 | D、24 |
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,E是PB的中点,AB=2AD=2CD=2,且二面角P-AC-E的大小为
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,E是PB的中点,AB=2AD=2CD=2,且二面角P-AC-E的大小为 四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,AA′⊥平面ABCD.
四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,AA′⊥平面ABCD.