Question

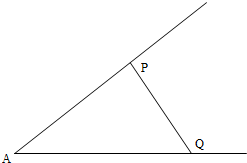如图，已知锐角∠A为定角，点P，Q分别在∠A的两边上，且△APQ的面积为定值S，当P，Q在什么位置时，PQ长最短．

Answer 1

考点：基本不等式

专题：不等式的解法及应用

分析：由S=

1

2

AP•AQ•sinA，可得AP•AQ=

2S

sinA

．在△APQ中，由余弦定理可得：PQ²=AP²+AQ²-2AP•AQcosA，再利用基本不等式即可得出．

解答： 解：∵S=

1

2

AP•AQ•sinA，∴AP•AQ=

2S

sinA

．
在△APQ中，由余弦定理可得：PQ²=AP²+AQ²-2AP•AQcosA≥2AP•AQ（1-cosA），
当且仅当AP=AQ=

2S sinA

时取等号．
∴当且仅当AP=AQ=

2S sinA

时，PQ最短为2

S(1-cosA) sinA

．

点评：本题考查了三角形的面积计算公式、余弦定理、基本不等式，考查了推理能力和计算能力，属于中档题．