题目内容
计算：（x+
）+（x2+
）+…+（xn+
）（x≠0，x≠1，y≠1）．
| 1 |
| y |
| 1 |
| y2 |
| 1 |
| yn |
考点：数列的求和
专题：计算题,等差数列与等比数列
分析：可运用分组求和，可将（x+
）+（x2+
）+…+（xn+
）写成（x+x2+x3+…+xn）+（
+
+
+…+
）由于x≠0，x≠1，y≠1，运用等比数列的求和公式即可．
| 1 |
| y |
| 1 |
| y2 |
| 1 |
| yn |
| 1 |
| y |
| 1 |
| y2 |
| 1 |
| y3 |
| 1 |
| yn |
解答：
解：∵x≠0，x≠1，y≠1，
∴（x+
）+（x2+
）+…+（xn+
）
=（x+x2+x3+…+xn）+（
+
+
+…+
）
=
+
=
+
．
∴（x+
| 1 |
| y |
| 1 |
| y2 |
| 1 |
| yn |
=（x+x2+x3+…+xn）+（
| 1 |
| y |
| 1 |
| y2 |
| 1 |
| y3 |
| 1 |
| yn |
=
| x(1-xn) |
| 1-x |
| ||||
1-
|
=
| x-xn+1 |
| 1-x |
| 1-y-n |
| y-1 |
点评：本题考查数列的求和方法：分组求和，分成两组均为等比数列，运用等比数列的求和，考查计算能力，属于基础题．
练习册系列答案
相关题目
若函数f（x）=asinx+
cosx在x=
处有最值，那么a等于（ ）
| 1 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设f（x）与g（x）是定义在R上的两个函数，若对任意x∈[a，b]，都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“密切函数”．若f（x）=x2-3x+4与g（x）=2x+t在[2，3]上时“密切函数”，则实数t的取值范围是（ ）
| A、[-3，-1] | ||||
B、[-
| ||||
C、[-
| ||||
D、[-3，-
|
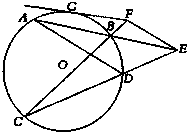已知：如图，圆O两弦AB与CD交于E，EF∥AD，EF与CB延长线交于F，FG切圆O于G．