题目内容
14．有一长、宽分别为50m、30m的游泳池，一名工作人员在池边巡视，某时刻出现在池边任一位置的可能性相同．一人在池中心（对角线交点）处呼唤工作人员，其声音可传出$15\sqrt{2}m$，则工作人员能及时听到呼唤（出现在声音可传到区域）的概率是（ ）| A． | $\frac{3}{4}$ | B． | $\frac{3}{8}$ | C． | $\frac{3π}{16}$ | D． | $\frac{12+3π}{32}$ |
分析 由题意可知所有可能结果用周长160表示，事件发生的结果可用两条线段的长度和60表示，即可求得．
解答 
解：当该人在池中心位置时，呼唤工作人员的声音可以传$15\sqrt{2}m$，那么当构成如图所示的三角形时，工作人员才能及时的听到呼唤声，
所有可能结果用周长160表示，事件发生的结果可用两条线段的长度和60表示，$P=\frac{60}{160}=\frac{3}{8}$．
故选B．
点评 本题考查几何概型，根据题意绘制出图形，利用数形结合，求得结果，属于中档题．
练习册系列答案
相关题目
6．从抛物线y2=4x的准线l上一点P引抛物线的两条切线PA，PB，A，B为切点，若直线AB的倾斜角为$\frac{π}{3}$，则P点的纵坐标为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | 2$\sqrt{3}$ |
3．已知A，B，P是双曲线mx2-ny2=1（m＞0，n＞0）上不同的三点，且A，B连线经过坐标原点，若直线PA，PB的斜率积为$\frac{2}{3}$，则该双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{15}}}{3}$ | C． | $\sqrt{2}$ | D． | $\frac{{\sqrt{6}}}{2}$ |
9．
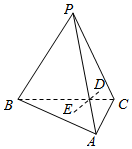三棱锥P-ABC中，D、E分别是三角形PAC和三角形ABC的外心，则下列判断一定正确的是（ ）
三棱锥P-ABC中，D、E分别是三角形PAC和三角形ABC的外心，则下列判断一定正确的是（ ）| A． | DE∥PB | B． | 当AB=BC且PA=AC时DE∥PB | ||
| C． | 当且仅当AB=BC且PA=AC时，DE⊥AC | D． | DE⊥AC |
3．
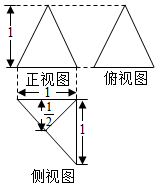某几何体的三视图如图所示，其中正视图和侧视图是全等的等腰三角形，现从该几何体的实心外接球中挖去该几何体，则剩余几何体的体积是（ ）
某几何体的三视图如图所示，其中正视图和侧视图是全等的等腰三角形，现从该几何体的实心外接球中挖去该几何体，则剩余几何体的体积是（ ）| A． | $\frac{9π}{4}$-$\frac{1}{6}$ | B． | $\frac{9π}{16}$-$\frac{1}{2}$ | C． | $\frac{9π}{16}$-$\frac{1}{6}$ | D． | $\frac{9π}{8}$-$\frac{1}{6}$ |