题目内容
6.从抛物线y2=4x的准线l上一点P引抛物线的两条切线PA,PB,A,B为切点,若直线AB的倾斜角为$\frac{π}{3}$,则P点的纵坐标为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
分析 利用直线AB的倾斜角为$\frac{π}{3}$,可得y1+y2=$\frac{4\sqrt{3}}{3}$.求出即切线PA的方程为y=$\frac{2}{{y}_{1}}$x+$\frac{1}{2}$y1,切线PB的方程为y=$\frac{2}{{y}_{2}}$x+$\frac{1}{2}$y2,y1、y2是方程t2-2yt+4x=0两个根,利用韦达定理,可得结论.
解答 解:设A(x1,y1),B(x2,y2),P(-1,y),则kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{4}{{y}_{1}+{y}_{2}}$,
∵直线AB的倾斜角为$\frac{π}{3}$,
∴$\frac{4}{{y}_{1}+{y}_{2}}$=$\sqrt{3}$,
∴y1+y2=$\frac{4\sqrt{3}}{3}$.
切线PA的方程为y-y1=$\frac{2}{{y}_{1}}$(x-x1),切线PB的方程为y-y2=$\frac{2}{{y}_{2}}$(x-x2),
即切线PA的方程为y=$\frac{2}{{y}_{1}}$x+$\frac{1}{2}$y1,切线PB的方程为y=$\frac{2}{{y}_{2}}$x+$\frac{1}{2}$y2.
∴y1、y2是方程t2-2yt+4x=0两个根,
∴y1+y2=2y=$\frac{4\sqrt{3}}{3}$.
∴y=$\frac{2\sqrt{3}}{3}$.
故选:B.
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b,若△ABC的面积为S=$\frac{{\sqrt{3}}}{12}$c,则ab的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 3 |
14.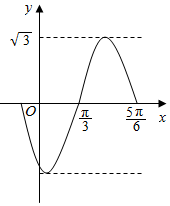 已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )
已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )
 已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )
已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
11.已知向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|$=2,$\overrightarrow a$•$({\overrightarrow b-\overrightarrow a})$=-3,则$\overrightarrow b$在$\overrightarrow a$方向上的投影为( )
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
14.有一长、宽分别为50m、30m的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出$15\sqrt{2}m$,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3π}{16}$ | D. | $\frac{12+3π}{32}$ |
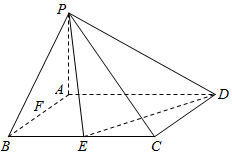 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点. 型和20台
型和20台 型电脑的利润为4000元,销售20台
型电脑的利润为4000元,销售20台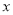 台,这100台电脑的销售总利润为
台,这100台电脑的销售总利润为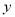 元.
元.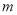 (
(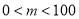 )元,且限定商店最多购进
)元,且限定商店最多购进